Ant Lion Optimizer：一种新型自然启发式算法

需积分: 17 156 浏览量更新于2024-07-16 收藏 2.83MB PDF 举报

《蚁狮优化器》(The Ant Lion Optimizer) 本文提出了一种新的自然启发式算法——蚁狮优化器(ANT Lion Optimizer，ALO)，该算法模仿了自然界中蚁狮捕猎的机制。蚁狮捕猎的过程包括五个主要步骤：蚂蚁的随机行走、陷阱构建、蚂蚁落入陷阱、捕获猎物以及陷阱的再构建。ALO算法在三个阶段进行了基准测试。首先，通过19个数学函数测试了ALO的不同特性，以评估其在探索性、局部最优避免、利用性和收敛性方面的表现。其次，ALO被应用于解决三个经典的工程问题，即三杆桁架设计、悬臂梁设计和齿轮传动设计，显示了它在处理具有不同搜索空间的约束问题时的优势。最后，通过对两个船用螺旋桨形状的优化，ALO展示了其在解决具有未知搜索空间的真实问题上的适用性。ALO算法在这些测试中表现出色，提供了非常有竞争力的结果，并在大多数经典工程问题上找到了更优的解决方案。 ALO算法的独特之处在于它能够有效地平衡全局搜索和局部搜索，这使得它在解决复杂优化问题时具有较高的性能。在与文献中各种算法的比较中，ALO展现出了优秀的探索能力和避免局部最优的能力，同时能快速收敛到全局最优解。对于工程问题的求解，ALO不仅在无约束优化中表现良好，而且在处理有约束问题时也显示出强大的能力。此外，ALO在解决实际的船用螺旋桨设计问题时，证明了其在面对未知搜索空间时的适应性。这种适应性对于实际应用至关重要，因为它允许算法在没有先验知识的情况下，找到最佳的设计解决方案。作者在http://www.alimirjalili.com/ALO.html提供了ALO算法的源代码，使得研究者和工程师可以进一步研究和应用这一算法。总结来说，蚁狮优化器(ALO)是一种创新的自然启发式算法，它通过模拟生物界中蚁狮的捕猎策略来解决优化问题。ALO在数学函数测试、工程问题求解以及实际问题优化中都表现出优越的性能，尤其是在处理约束条件下的优化问题上。由于其公开的源代码，ALO为研究者提供了一个工具，以进一步探索和改进优化算法，从而推动了优化领域的进步。

2.2.2. Trapping in antlion’s pits

As discussed above, random walks of ants are affected by

antlions’ traps. In order to mathematically model this assumption,

the following equations are proposed:

¼ Antlion

þ c

ð2:8Þ

¼ Antlion

þ d

ð2:9Þ

where c

is the minimum of all variables at t-th iteration, d

indicates

the vector including the maximum of all variables at t-th iteration,

is the minimum of all variables for i-th ant, d

is the maximum of

all variables for i-th ant, and Antlion

shows the position of the

selected j-th antlion at t-th iteration.

Eqs. (2.8) and (2.9) show that ants randomly walk in a hyper

sphere deﬁned by the vectors c and d around a selected antlion.

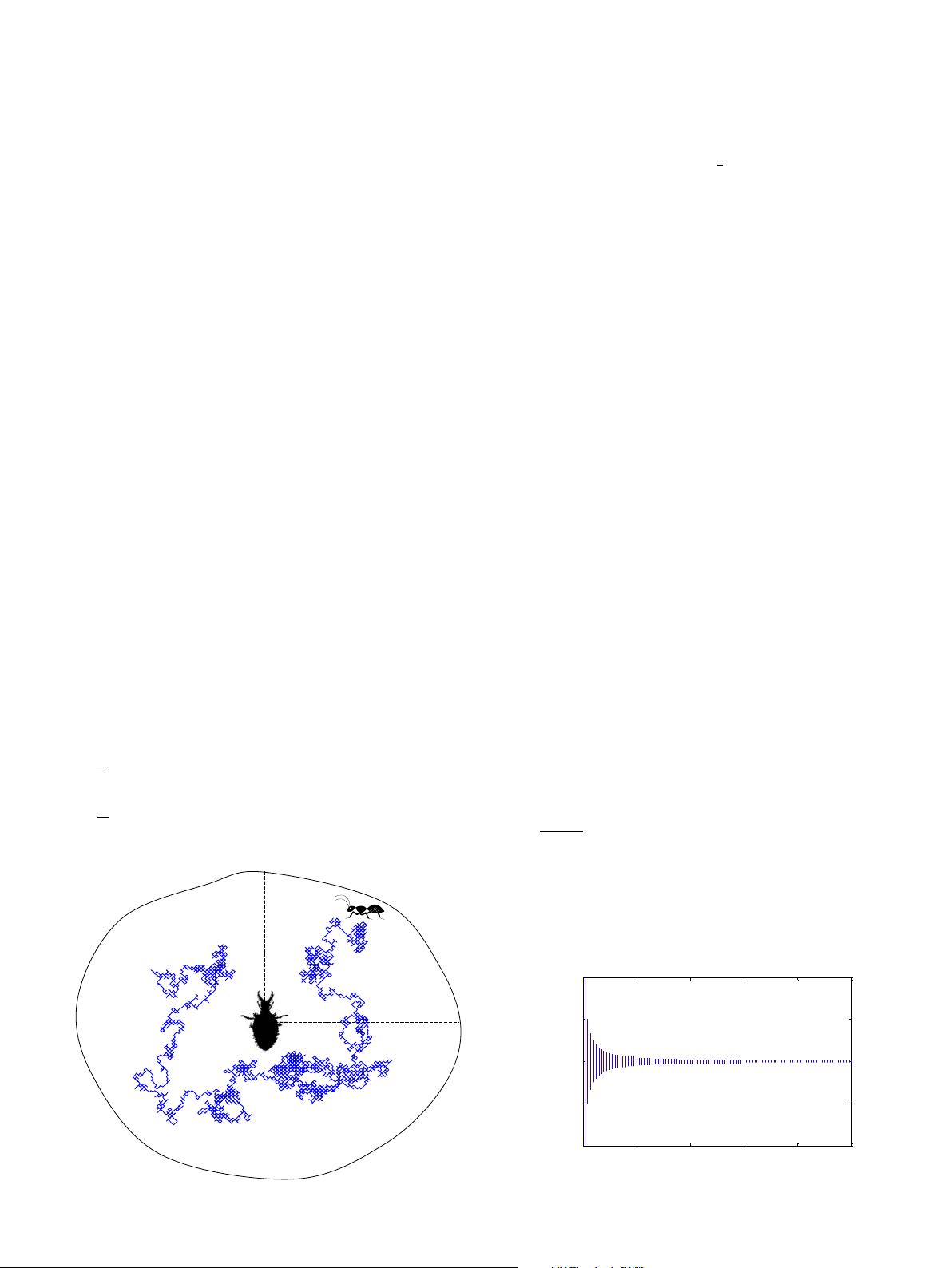
A conceptual model of this behaviour is illustrated in Fig. 3.

Fig. 3 shows a two-dimensional search space. It may be

observed that ants are required to move within a hypersphere

around a selected antlion.

2.2.3. Building trap

In order to model the antlions’s hunting capability, a roulette

wheel is employed. As Fig. 3 show ants are assumed to be trapped

in only one selected antlion. The ALO algorithm is required to uti-

lize a roulette wheel operator for selecting antlions based of their

ﬁtness during optimization. This mechanism gives high chances

to the ﬁtter antlions for catching ants.

2.2.4. Sliding ants towards antlion

With the mechanisms proposed so far, antlions are able to build

traps proportional to their ﬁtness and ants are required to move

randomly. However, antlions shoot sands outwards the center of

the pit once they realize that an ant is in the trap. This behaviour

slides down the trapped ant that is trying to escape. For mathemat-

ically modelling this behaviour, the radius of ants’s random walks

hyper-sphere is decreased adaptively. The following equations are

proposed in this regard:

ð2:10Þ

ð2:11Þ

where I is a ratio, c

is the minimum of all variables at t-th iteration,

and d

indicates the vector including the maximum of all variables

at t-th iteration.

In Eqs. (2.10) and (2.11), I ¼ 10

where t is the current itera-

tion, T is the maximum number of iterations, and w is a constant

deﬁned based on the current iteration (w = 2 when t > 0.1T, w =3

when t > 0.5T, w = 4 when t > 0.75T, w = 5 when t > 0.9T, and

w = 6 when t > 0.95T). Basically, the constant w can adjust the

accuracy level of exploitation.

Fig. 4 also shows the decreasing behaviour using Eqs. (2.10) and

(2.11). These equations shrink the radius of updating ant’s

positions and mimics sliding process of ant inside the pits. This

guarantees exploitation of search space.

2.2.5. Catching prey and re-building the pit

The ﬁnal stage of hunt is when an ant reaches the bottom of the

pit and is caught in the antlion’s jaw. After this stage, the antlion

pulls the ant inside the sand and consumes its body. For mimicking

this process, it is assumed that catching prey occur when ants

becomes ﬁtter (goes inside sand) than its corresponding antlion.

An antlion is then required to update its position to the latest posi-

tion of the hunted ant to enhance its chance of catching new prey.

The following equation is proposed in this regard:

Antlion

¼ Ant

if f ðAnt

Þ > f Antlion



ð2:12Þ

where t shows the current iteration, Antlion

shows the position of

selected j-th antlion at t-th iteration, and Ant

indicates the position

of i-th ant at t-th iteration.

2.2.6. Elitism

Elitism is an important characteristic of evolutionary algo-

rithms that allows them to maintain the best solution(s) obtained

at any stage of optimization process. In this study the best antlion

obtained so far in each iteration is saved and considered as an elite.

Since the elite is the ﬁttest antlion, it should be able to affect the

movements of all the ants during iterations. Therefore, it is

assumed that every ant randomly walks around a selected antlion

by the roulette wheel and the elite simultaneously as follows:

Ant

þ R

ð2:13Þ

where R

is the random walk around the antlion selected by the

roulette wheel at t-th iteration, R

is the random walk around the

elite at t-th iteration, and Ant

indicates the position of i-th ant at

t-th iteration.

Fig. 3. Random walk of an ant inside an antlion’s trap.

0 20 40 60 80 100

-100

-50

100

Iteration (t)

lower bound (c) & upper bound (d)

Fig. 4. Adaptive lower (c

) and upper (d

) bounds.

S. Mirjalili / Advances in Engineering Software 83 (2015) 80–98

剩余18页未读，继续阅读

SparkQiang

粉丝: 62
资源: 123

Ant Lion Optimizer：一种新型自然启发式算法

蚁狮优化器 Ant Lion Optimizer

Ant Lion Optimizer

Ant Lion Optimizer 工具箱：Ant Lion Optimizer (ALO) 算法的工具箱-matlab开发

New-folder.zip_Ant Lion_Ant lion optimizer_ant lion algorithm_li

Multi-objective Ant Lion Optimizer (MOALO)：最近提出的Ant Lion Optimizer的多目标版本-matlab开发

New-folder.rar_Ant Lion_Ant lion optimizer_lion_lion algorithm

Multi-objective ant lion optimizer

ug1333-ai-optimizer.pdf

Consulting Report network audit-WAN Optimizer.pdf

Windows2003+IIS6.0 下安装Zend Optimizer.pdf

最新资源