动态规划加速：四边形不等式原理与应用

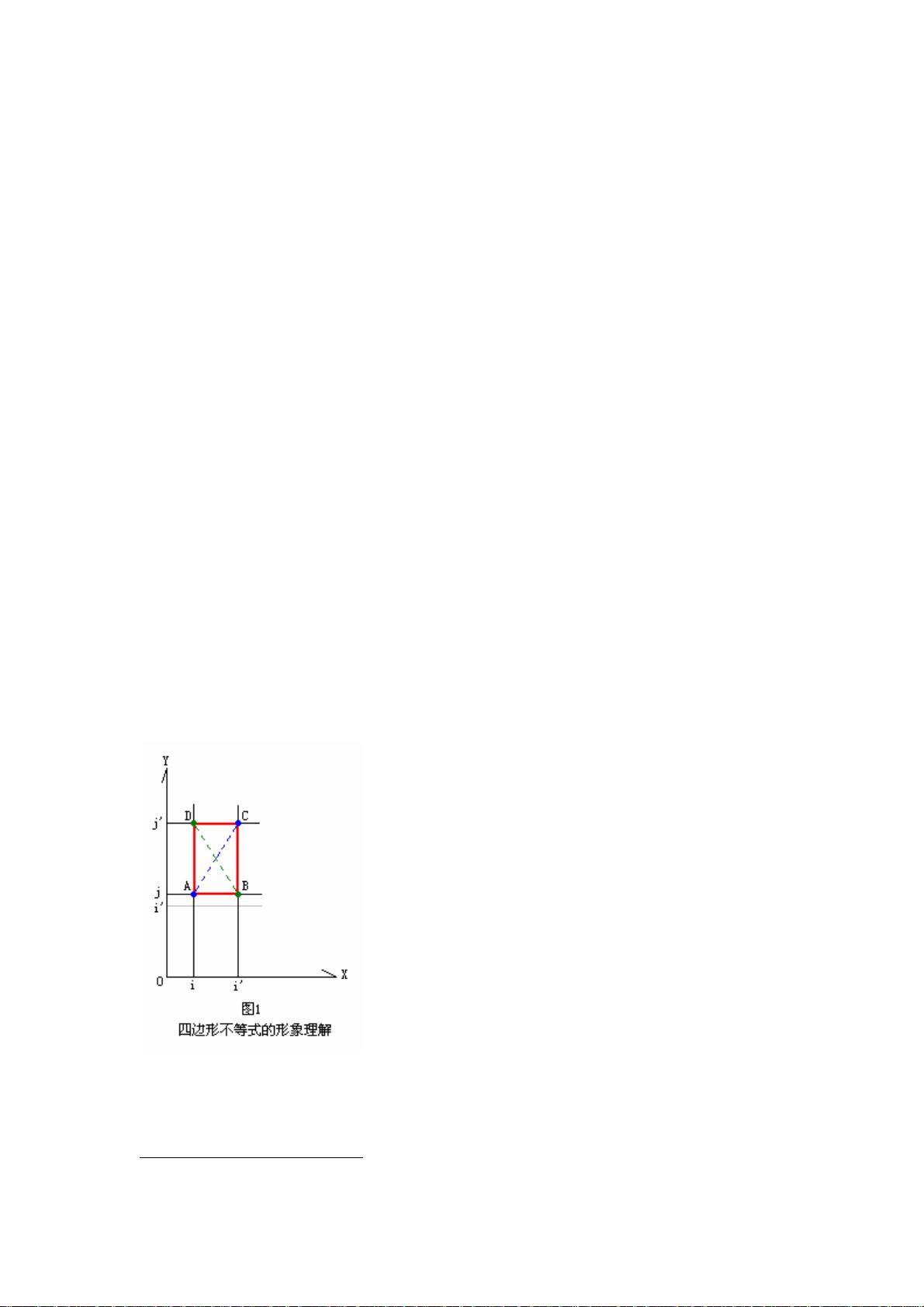
"DP优化之四边形不等式，用于加速动态规划解题，涉及区间包含的单调性和四边形不等式的关系" 在动态规划(DP)中，四边形不等式是一个重要的优化工具，它可以帮助我们减少计算量，提高算法效率。四边形不等式在处理具有特定性质的状态转移方程时特别有用，这些方程通常涉及寻找最小值或最大值。在描述具体问题时，例如"最小代价子母树"问题，我们通常会遇到以下状态转移方程： \( m_{ij} = \min\limits_{k=0}^{j-1}(m_{ik} + w_{kj}) \) 这里，\( m_{ij} \) 表示从状态 i 到状态 j 的最优成本，\( w_{kj} \) 是从状态 k 到状态 j 的代价。如果函数 \( w \) 满足四边形不等式，即对于任意 \( i \leq j < j' \leq i' \)，都有： \( w_{ij} + w_{i'j'} \leq w_{ii'} + w_{jj'} \) 这意味着，四边形的对角线端点之间的权值之和总是小于等于另一对对角线端点的权值之和。 四边形不等式的意义在于，它揭示了函数 \( w \) 在二维空间中的局部平滑性。在动态规划的上下文中，这意味着当我们尝试通过中间状态 \( k \) 从状态 \( i \) 更新到状态 \( j \) 时，我们可以跳过状态 \( k \)，直接从 \( i \) 更新到 \( j' \)，而不会增加总代价，只要 \( w \) 满足四边形不等式。 证明四边形不等式对 \( m \) 也成立，即 \( m_{ij} + m_{i'j'} \leq m_{ii'} + m_{jj'} \)，可以使用归纳法。基本思想是，当 \( i = i' \) 或 \( j = j' \) 时，不等式显然成立。然后，我们可以假设对于 \( l < j \leq j' \)，四边形不等式已经成立，并尝试证明 \( j = l+1 \) 的情况。这样，我们可以通过递归地应用状态转移方程和已知的四边形不等式来推导出新的不等式。 在实际应用中，理解并利用四边形不等式能够帮助我们设计更有效的动态规划解决方案，例如通过剪枝减少不必要的计算，或者构建更高效的记忆化搜索。这种技术尤其适用于那些状态空间巨大，直接穷举所有可能状态会导致时间复杂度过高的问题。通过巧妙地应用四边形不等式，可以显著降低算法的时间复杂度，提升算法性能，使得原本难以解决的大规模问题变得可行。