MATLAB中的常微分方程求解与数值解法

微分方程在众多领域中发挥着核心作用，用于建立数学模型以研究各种现象，如物理振动、电路响应、热传导、抛体运动和人口动态等。然而，解析解并非所有情况都能获得，特别是在处理变系数或非线性方程时。因此，数值解法成为解决实际问题的关键手段。 MATLAB提供了一套强大的工具箱，其中的dsolve函数支持常微分方程（组）的符号求解，这对于理解和验证理论分析极为重要。以下是MATLAB中关于常微分方程求解的要点： 1. **符号求解**: - `dsolve`函数是MATLAB中用于符号求解的基础工具。调用格式包括两种： - 调用格式一：`S=dsolve('eqn', 'var')` 这里，`eqn`是以符号形式表示的一阶或更高阶的常微分方程，如`D^2y(t) + Dy(t) + y(t) = 0`，`var`默认为时间变量`t`。 - 调用格式二：当有多个方程需要求解时，可以传递多个方程，如`S=dsolve(['eqn1', 'eqn2'], 'var')`。 2. **求特定解**: - 特殊情况下，如果知道初始条件或边界条件，可以提供额外参数，如`S=dsolve('eqn', 'condition1', ..., 'var')`。这用于获取满足特定条件的特解。 3. **线性常微分方程组**: - 对于线性常微分方程组，MATLAB提供了一个名为`qcxxcwz.m`的函数，用于求解齐次线性方程组。该函数接受系数矩阵`A`作为输入，通过计算特征值和特征向量，计算出解的表达式。 4. 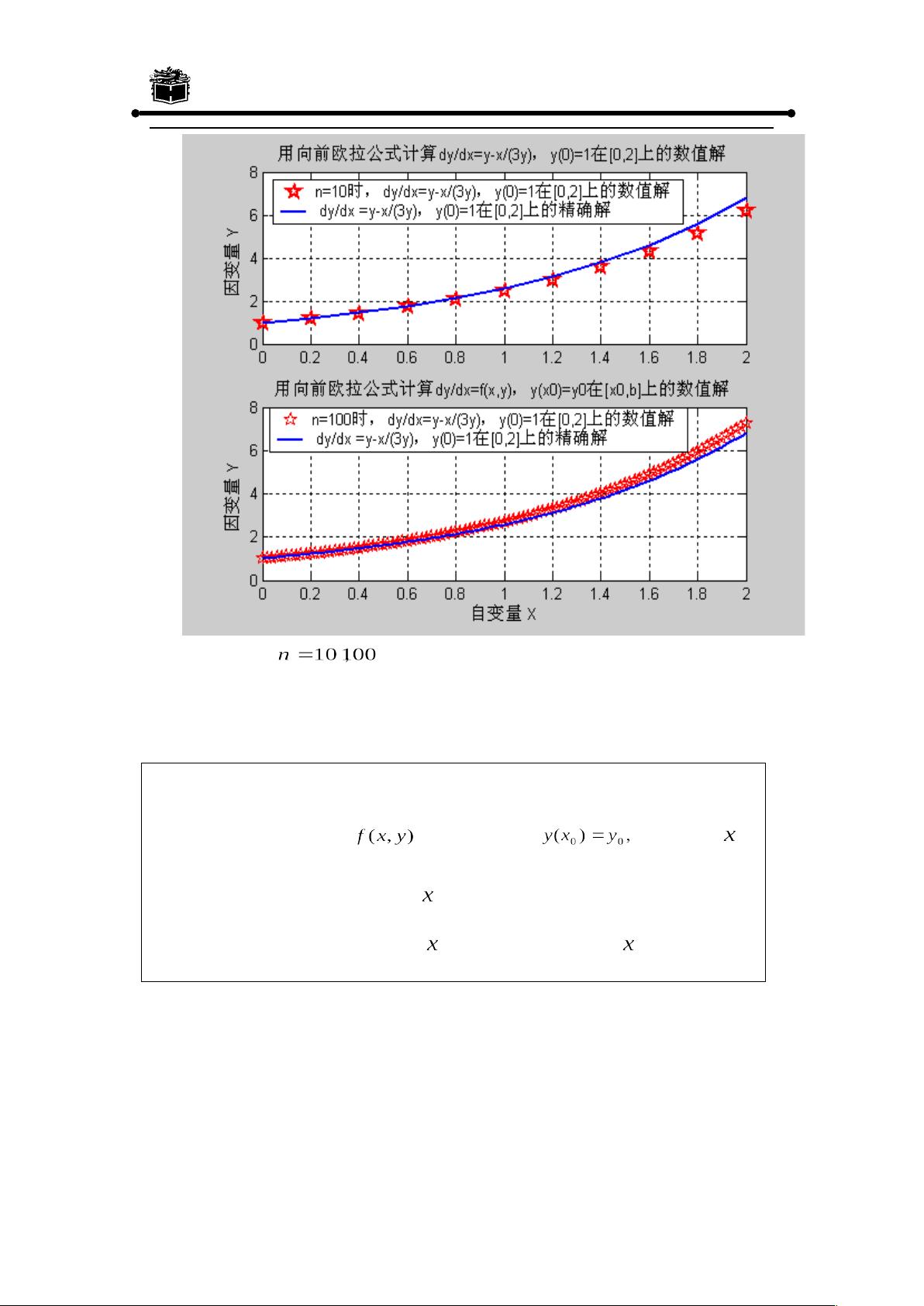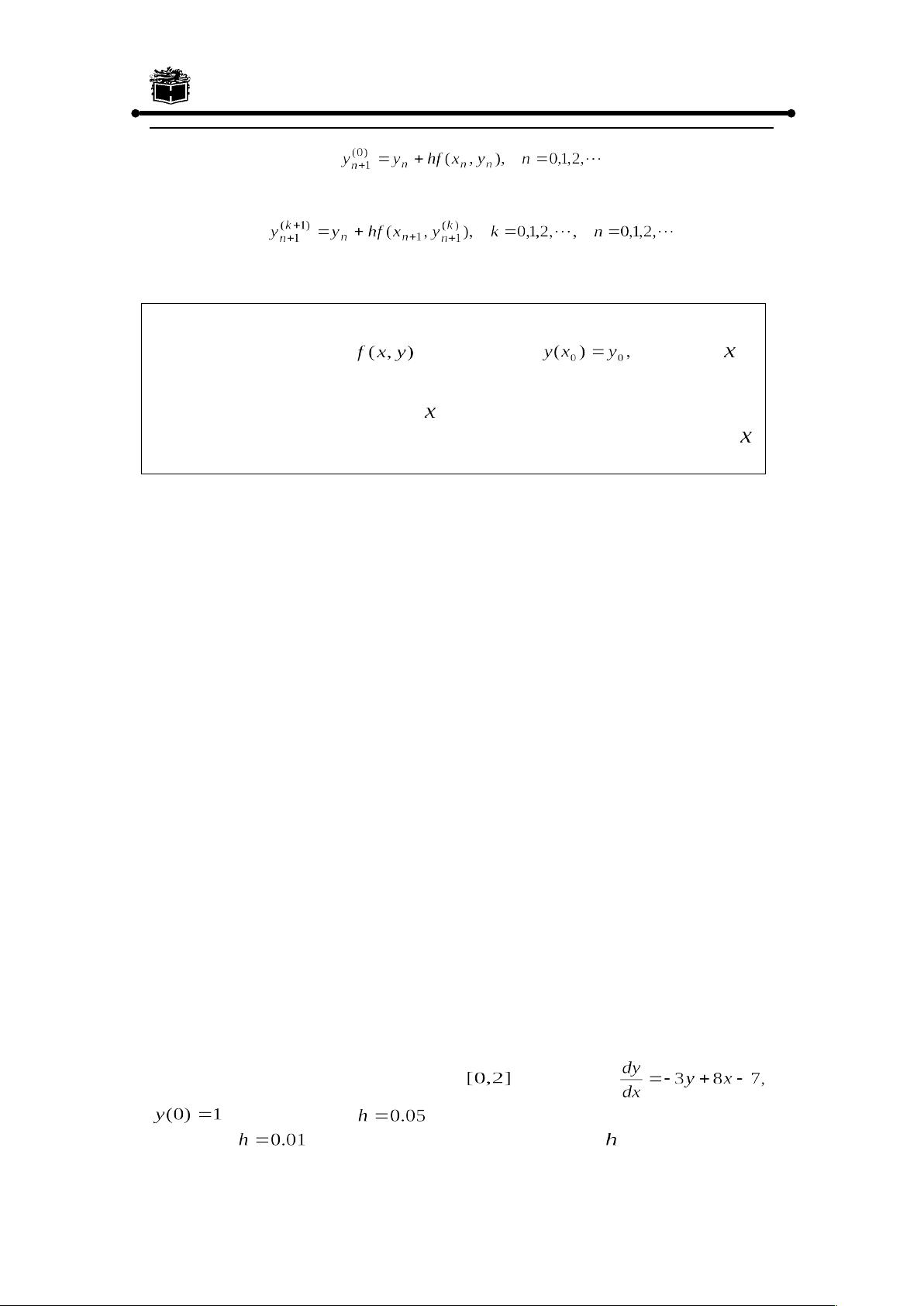**数值解法**: - 除了符号解，MATLAB还支持数值方法来求解微分方程，这对于无法找到解析解或需要精确数值结果的情况尤其适用。尽管数值解法不直接涉及解析表达，但它是微分方程建模的重要组成部分，如使用欧拉方法（Euler method）进行近似计算。 5. **欧拉方法示例**: - MATLAB中包含欧拉方法的实现，如向前欧拉公式，它是一种基础的数值积分方法，可以用来近似连续微分方程的解。这种方法的优点是简单易实现，但可能会引入较大的误差，适用于简单的初值问题。 总结来说，MATLAB中的dsolve函数为微分方程求解提供了符号解和数值解的工具，帮助科研人员和工程师在实际问题中有效地应用微分方程模型，无论是理论研究还是数值模拟，都扮演了关键角色。通过理解和熟练掌握这些功能，用户可以更好地解决实际问题中的复杂数学模型。