图像处理：霍夫变换(Hough Transform)原理与应用

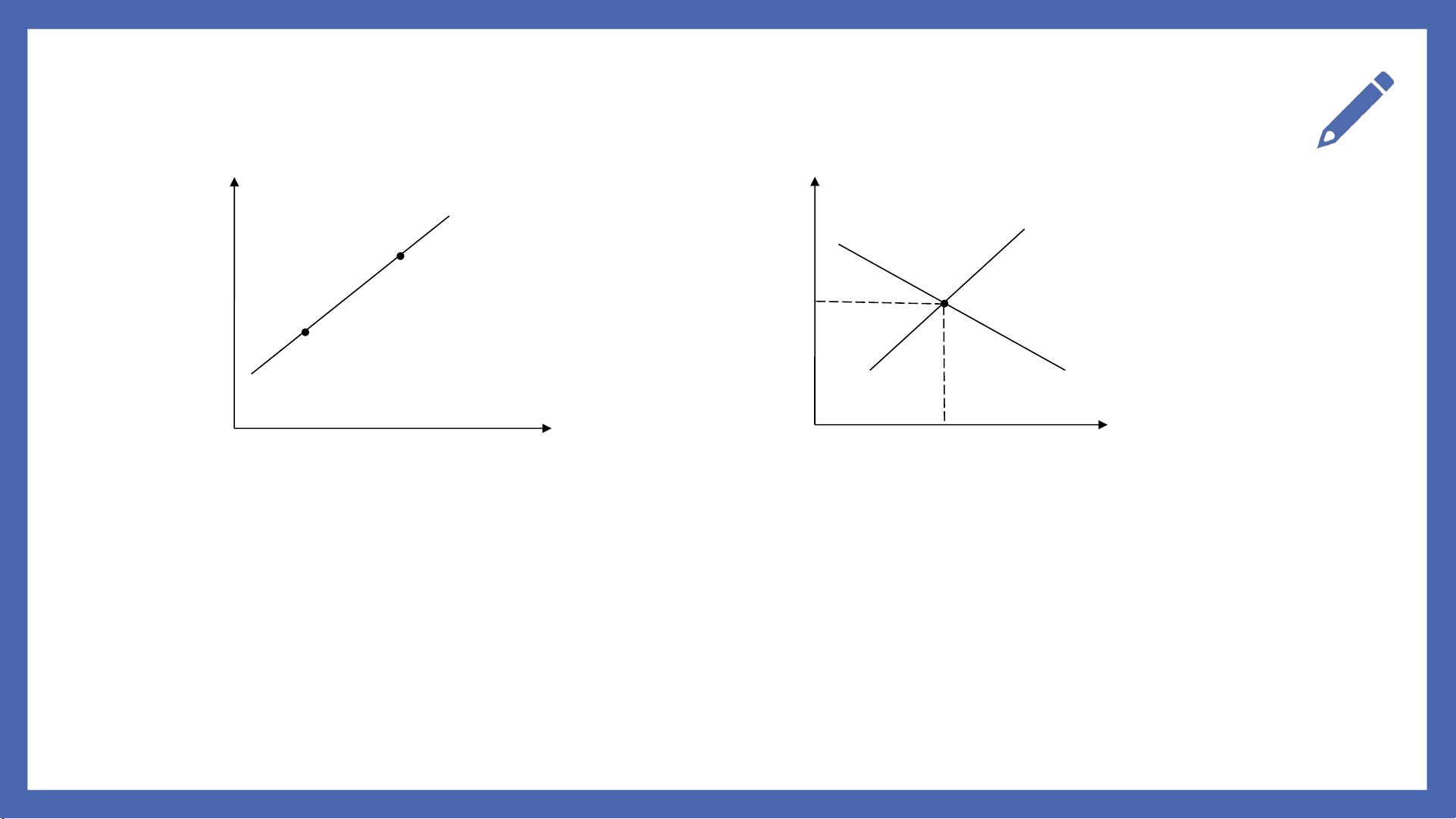
"这篇资料详细介绍了Hough变换的概念和应用，包括其基本思想、基本原理以及执行步骤。通过MATLAB程序来阐述了如何利用霍夫变换进行直线检测，转换图像空间中的直线检测问题为参数空间中对点的检测问题。" Hough变换是一种在图像处理领域中用于检测直线、圆等几何形状的算法。该变换的核心思想是将二维图像空间的直线映射到一维参数空间的点，使得图像中同一直线上的像素点在参数空间中对应于一个高峰，从而可以通过查找参数空间中的峰值来找到图像中的直线。 1. **基本思想**： Hough变换的基本思想是将图像中的点转换到参数空间。在图像空间(X-Y)中，一条直线可以由两点决定，即y = ax + b，而在参数空间(P-Q)中，这条直线被表示为一对参数(a, b)。通过Hough变换，图像空间中所有属于某直线的点都会在参数空间中对应到同一点，即参数空间的峰值。因此，检测图像中的直线就转换成了在参数空间寻找峰值的过程。 2. **基本原理**： 在图像空间中，一条通过点(xi, yi)的直线y = ax + b可以转换为参数空间的线性方程b = -ax + yi，其中a是斜率，b是截距。当多条这样的线在参数空间相交于同一点(a', b')时，意味着图像空间中有过这个点的多条直线，这在实际中对应于一条真实存在的直线。 3. **基本步骤**： - 初始化：在参数空间创建一个二维数组A，数组大小对应于可能的斜率和截距范围，并将所有元素设置为0。 - 计算：遍历图像空间中的每一个点，对于每个点，计算所有可能的斜率a和截距b，更新对应于(a, b)位置的数组元素A[a, b]，将其加1。 - 检测：遍历数组A，找出值最大的点，这些点代表了图像空间中可能存在直线的参数。 4. **MATLAB程序的应用**： MATLAB提供了实现Hough变换的函数，可以方便地进行直线检测。通过计算图像中每个非背景点对应的所有可能参数空间点，并累加计数，最终形成一个累积图像，其中的峰值对应于图像中的直线。 5. **优化技巧**： 在实际应用中，为了提高效率，通常会将参数空间离散化，将连续的斜率和截距范围划分成多个网格。然后，对于每个图像空间的点，只计算离散网格内的参数，并对相应网格的计数器增加。 6. **其他形状检测**： 虽然这里主要讨论了直线检测，但Hough变换也可扩展到检测其他形状，例如圆，只需改变参数空间的表示方式。 Hough变换是计算机视觉中一种强大的工具，尤其适用于在噪声环境中检测几何形状。通过理解和应用Hough变换，可以有效地在图像分析和处理中识别和提取关键特征。