WebGL 2D 矩阵：变换顺序问题的矩阵解决方案

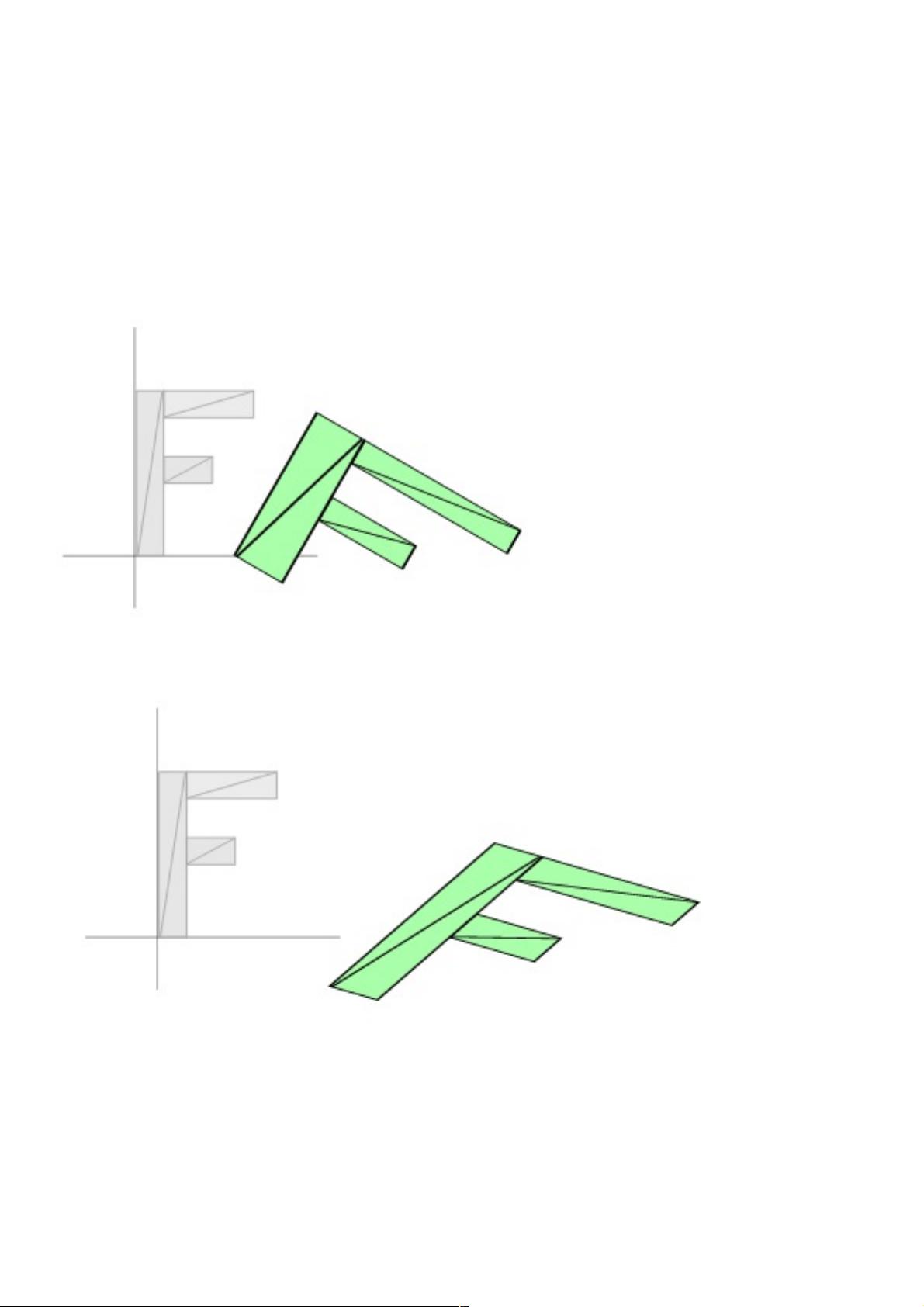
WebGL-2D-矩阵是一种在WebGL编程中处理2D图形变换的关键技术，它允许开发者在统一的矩阵运算中完成平移、旋转和缩放等操作，从而避免了传统顺序执行时可能出现的问题。在WebGL中，2D变换通常涉及3x3的矩阵，虽然看似复杂，但其实背后有严谨的数学原理支撑。 在处理2D图形时，一个3x3的矩阵被用于存储变换信息，其结构类似于一个3行3列的网格，其中包含x轴和y轴的移动、旋转和缩放参数。每个位置的坐标由x和y表示，但为了保持一致性，还需要添加一个额外的z值，通常设置为1，这有助于矩阵乘法的运算。 平移变换使用矩阵来表示，通过构造包含平移量（tx, ty）的矩阵，并进行矩阵乘法简化为简单的加法，如`newX = x + tx` 和 `newY = y + ty`，与传统的平移代码类似，但更具通用性和灵活性。 旋转则是利用正弦和余弦函数来表示角度，构建矩阵后进行矩阵乘法，结果为`newX = x * cos(angle) + y * sin(angle)` 和 `newY = x * -sin(angle) + y * cos(angle)`，这种方法确保了旋转的精确性。 缩放变换则使用两个缩放因子(sx, sy)，构建矩阵后计算`newX = x * sx` 和 `newY = y * sy`，这与之前的缩放操作一致，但矩阵形式提供了统一的处理方式。 这种矩阵方法的意义在于，无论平移、旋转还是缩放的顺序如何改变，只要矩阵运算的顺序保持不变，最终的结果就会保持一致。这样不仅减少了代码复杂性，还提高了代码的可维护性和可复用性。通过使用矩阵，开发人员可以在WebGL中高效地处理2D图形的变换，提升了图形渲染的精确性和效率。