"傅里叶变换引言：周期与非周期信号的频域分析"

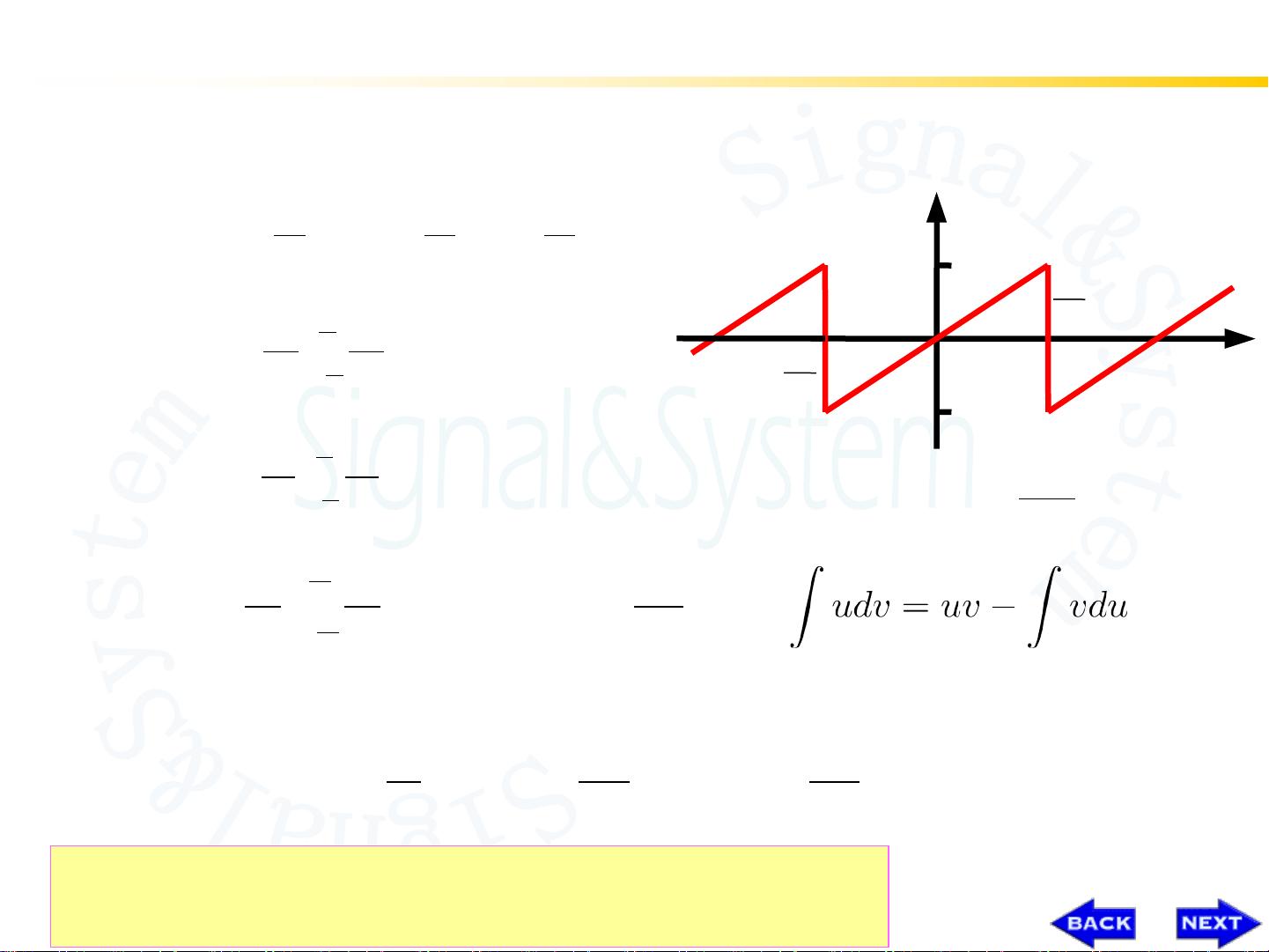
傅里叶变换在信号与系统分析中扮演着至关重要的角色。本章主要讨论了周期信号和非周期信号在频域上的表示与分析，包括周期信号的傅里叶级数分析，典型周期信号的傅里叶级数表示，以及非周期信号的傅里叶变换的基本原理和性质。 在引言部分，我们介绍了傅里叶变换的基本概念和历史背景，包括Jean Baptise Joseph Fourier对周期信号傅里叶级数和非周期信号傅里叶变换的贡献。他指出，周期信号可以表示为正弦信号的加权和，而非周期信号可以用正弦信号的加权积分表示。这一思想为傅里叶变换的发展奠定了基础。 在第三章中，我们详细讨论了周期信号的傅里叶级数分析和非周期信号的傅里叶变换。周期信号可以用一组正弦和余弦函数的线性组合表示，这就是傅里叶级数。通过计算各个频率成分的权重系数，我们可以将周期信号在频域上进行分解和分析。而非周期信号的傅里叶变换则是通过积分的方式将信号从时域转换到频域，得到信号的频谱密度分布。这种频域分析方法对于理解信号的频率成分和频率响应非常重要。 我们还讨论了典型非周期信号如冲激函数和阶跃函数的傅里叶变换，以及傅里叶变换的基本性质和卷积特性。冲激函数的傅里叶变换是一个常数，而阶跃函数的傅里叶变换则是一个带有频率偏移的正弦函数。傅里叶变换的性质包括线性性、频移性、频率缩放性等，这些性质在信号处理和系统分析中起着至关重要的作用。 在本章末尾，我们还介绍了抽样信号的傅里叶变换和抽样定理，探讨了信号在频域上的重构和还原。傅里叶变换在信号处理、通信系统、图像处理等领域有着广泛的应用，是理解和分析信号与系统行为的重要工具。 综上所述，本章涵盖了周期信号和非周期信号的傅里叶变换理论和方法，以及其在系统分析中的应用。通过学习这些内容，我们能够更深入地理解信号与系统的频域特性，为解决实际问题提供有效的工具和方法。傅里叶变换的研究不仅有理论意义，还有着广泛的实际应用，对于推动科学技术的发展具有重要的意义。