机器学习降维方法：K近邻与低维嵌入

第10章主要探讨了机器学习中的关键概念——降维与度量学习。降维是数据分析中常用的技术，旨在减少数据的维度，使得复杂问题在低维空间中更易于理解和处理。本章内容分为两个主要部分： 1. 特征选择与特征提取： - 特征选择：这是一种方法，它仅在原始特征集合中挑选最相关的部分，去除冗余或无关的信息。它基于统计或领域知识，通过评估每个特征与目标变量的相关性来决定哪些特征应该保留。 - 特征提取：与特征选择不同，特征提取是通过数学变换创造新的特征，这些新特征能够更好地捕捉数据的内在结构。例如，主成分分析（PCA）就是一种常用的特征提取技术，它通过线性变换将原始数据投影到一组新的坐标系中，新坐标系的轴按照方差的大小排序，从而实现降维。 2. 降维方法举例： - k近邻学习 (KNN)：作为懒惰学习算法，KNN在预测时依赖于训练样本的直接邻域，而非建立复杂的预测模型。它的核心是K值和距离度量的选择，这两个参数会直接影响分类效果。尽管其分类错误率通常不会超过贝叶斯最优分类器的两倍，但在高维数据中，由于“维数灾难”，KNN的效率会降低。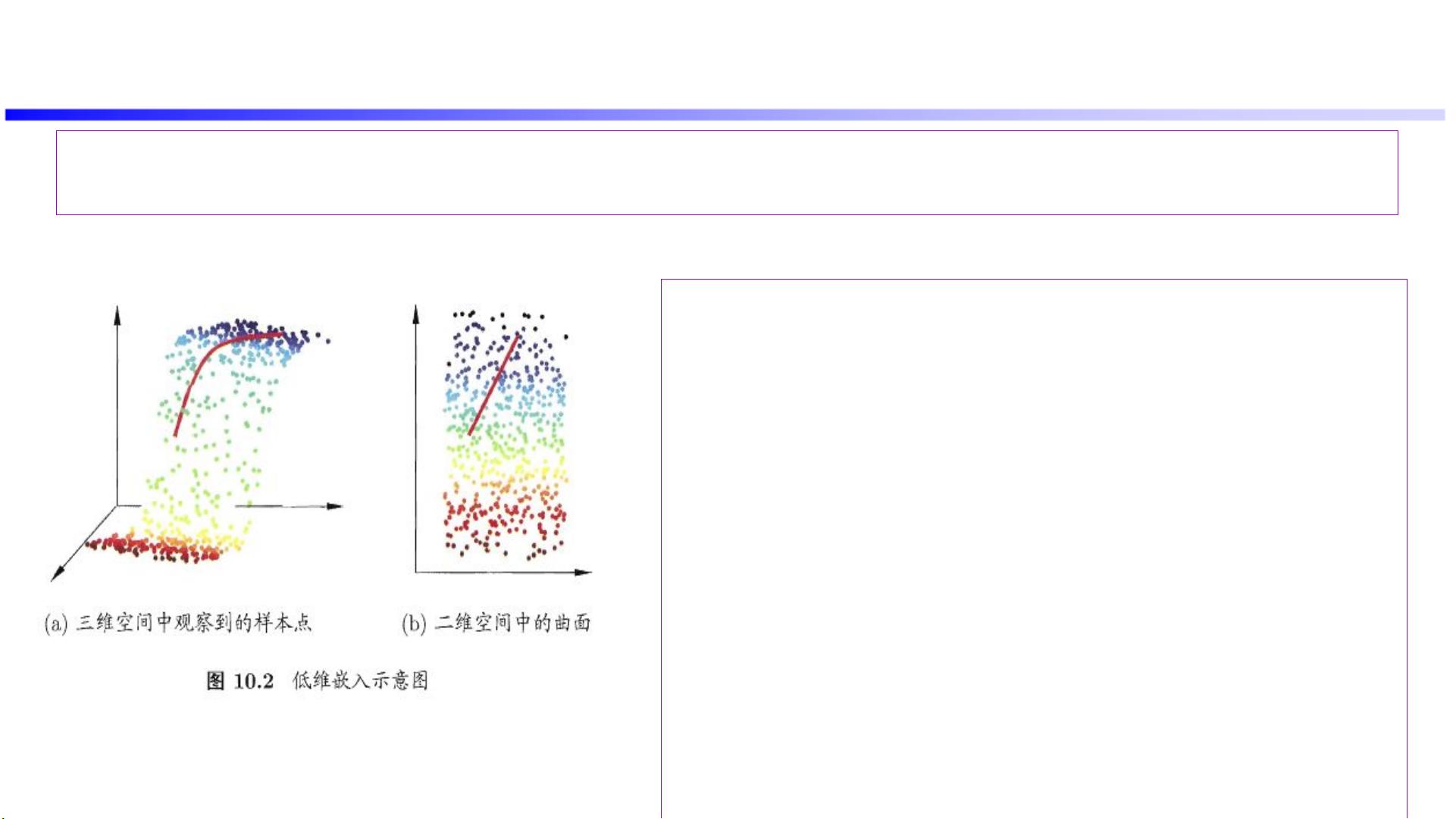 - 低维嵌入：针对高维数据稀疏性的问题，一种常见的解决方案是通过多维尺度(MDS)等方法进行降维，如MDS可以保持原始样本间距离的关系，使得在低维空间中数据的分布更加直观。然而，MDS仅关注训练数据，对新样本的表示有限，因此需要考虑如何扩展到整个空间。 - 线性降维：线性降维方法如主成分分析(PCA)和核化线性降维，通过线性变换寻找低维子空间，但可能受到特定约束，如保持正交性或稀疏性，这会影响最终的降维效果。 3. 度量学习：这部分关注的是如何设计有效的距离度量，以便在低维空间中更好地反映数据的内在结构。常见的度量学习方法包括等度量映射和局部线性嵌入，它们的目标是学习一种度量方式，使得数据点之间的相似性在降维后的空间中得到保留。 本章内容深入浅出地介绍了机器学习中降维技术的重要性以及具体实现方法，特别是如何通过特征选择和提取、低维嵌入和度量学习来处理高维数据的挑战。理解这些概念对于处理大规模、复杂的数据集至关重要。