朴素贝叶斯统计学习：原理与代码实现

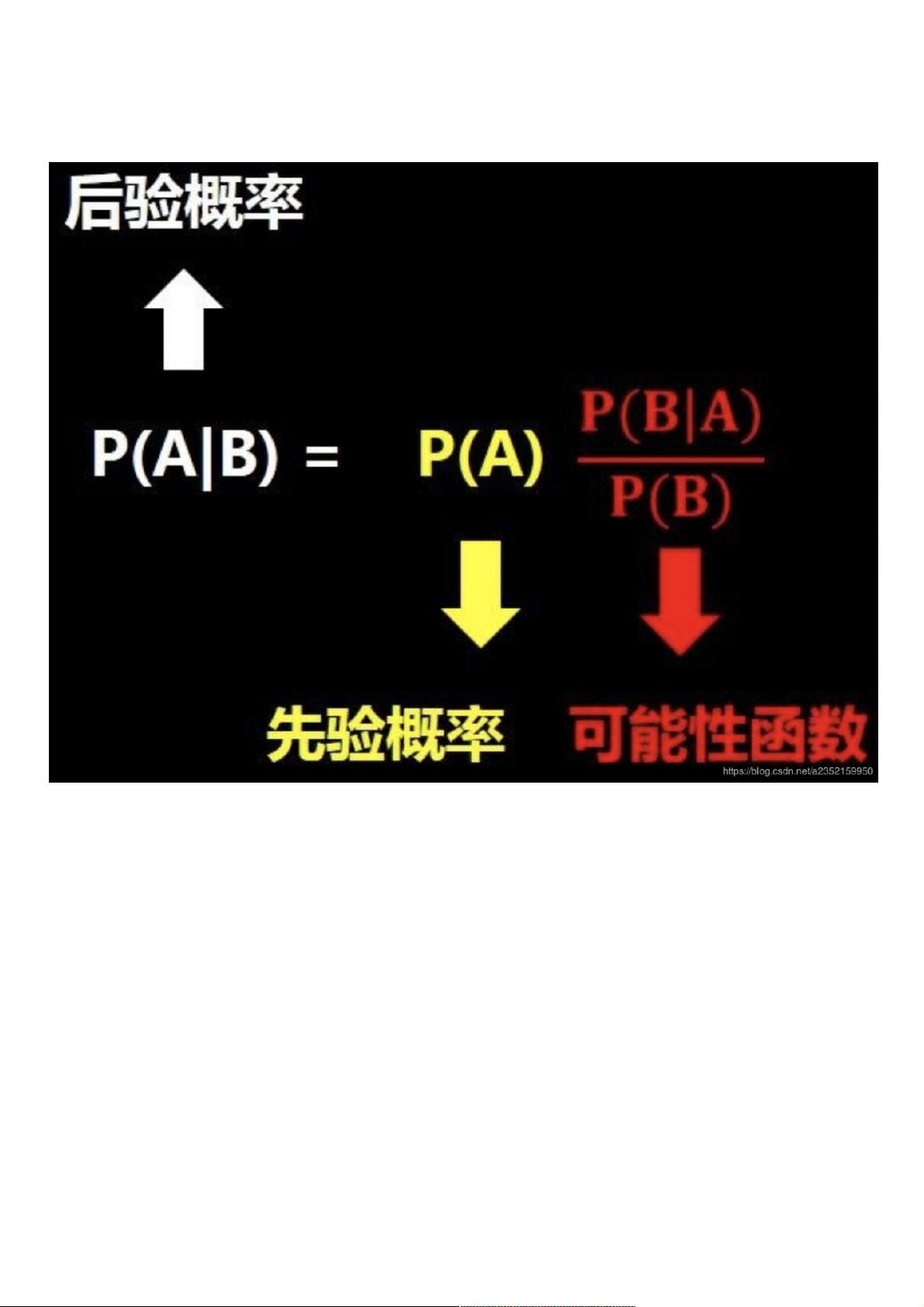
本文主要介绍了统计学习方法中的朴素贝叶斯理论，并通过代码复现来帮助理解。文章探讨了贝叶斯定理的基本概念，包括后验概率的推导、朴素贝叶斯条件以及极大似然估计在求解分类器中的应用。同时，提到了在实际操作中为避免概率为零和数值下溢出的问题，会采用贝叶斯估计和取对数的方法。 在统计学习中，朴素贝叶斯是一种基于贝叶斯定理的分类方法。贝叶斯定理阐述了在已知某些条件下，另一个事件发生的概率如何更新。公式表示为 P(A|B) = [P(B|A) * P(A)] / P(B)，其中 P(A|B) 是在事件 B 发生时事件 A 的后验概率，P(B|A) 是条件概率，P(A) 和 P(B) 分别是 A 和 B 的先验概率。朴素贝叶斯假设各个特征之间相互独立，虽然这在实际中并不总是成立，但简化后的模型在许多情况下仍能取得不错的效果。 在训练朴素贝叶斯分类器时，通常使用极大似然估计来求解各类别的先验概率和条件概率。极大似然估计允许我们根据已有的观测数据来估计参数的概率分布。然而，对于连续特征或稀疏数据，连乘项可能出现0，此时采用贝叶斯估计，通过对每个概率进行平滑处理，确保所有概率都不会为0，同时保持概率和为1。 此外，为了避免计算过程中因大量乘积导致的下溢出问题，通常会对概率取对数。对数操作不仅解决了数值稳定性问题，而且在比较概率大小时不会改变结果，因为对数函数是单调递增的。取对数后，即使原始概率很小，其对数值也会相对较大，计算机可以更准确地处理这些数值。 在实际应用中，例如文本分类或手写数字识别，朴素贝叶斯模型被广泛使用。文章中还提及使用 TensorFlow 加载和处理 MNIST 手写数字数据集的示例，这是机器学习领域的一个经典数据集，用于演示分类算法的性能。 朴素贝叶斯方法提供了一种简洁而有效的分类工具，尽管它的“朴素”假设在某些复杂场景下可能过于简化，但在许多实际问题中，这种方法依然表现出色。通过理解贝叶斯定理、极大似然估计和取对数等技术，我们可以更好地掌握朴素贝叶斯分类器的工作原理，并将其应用于实际的机器学习项目中。