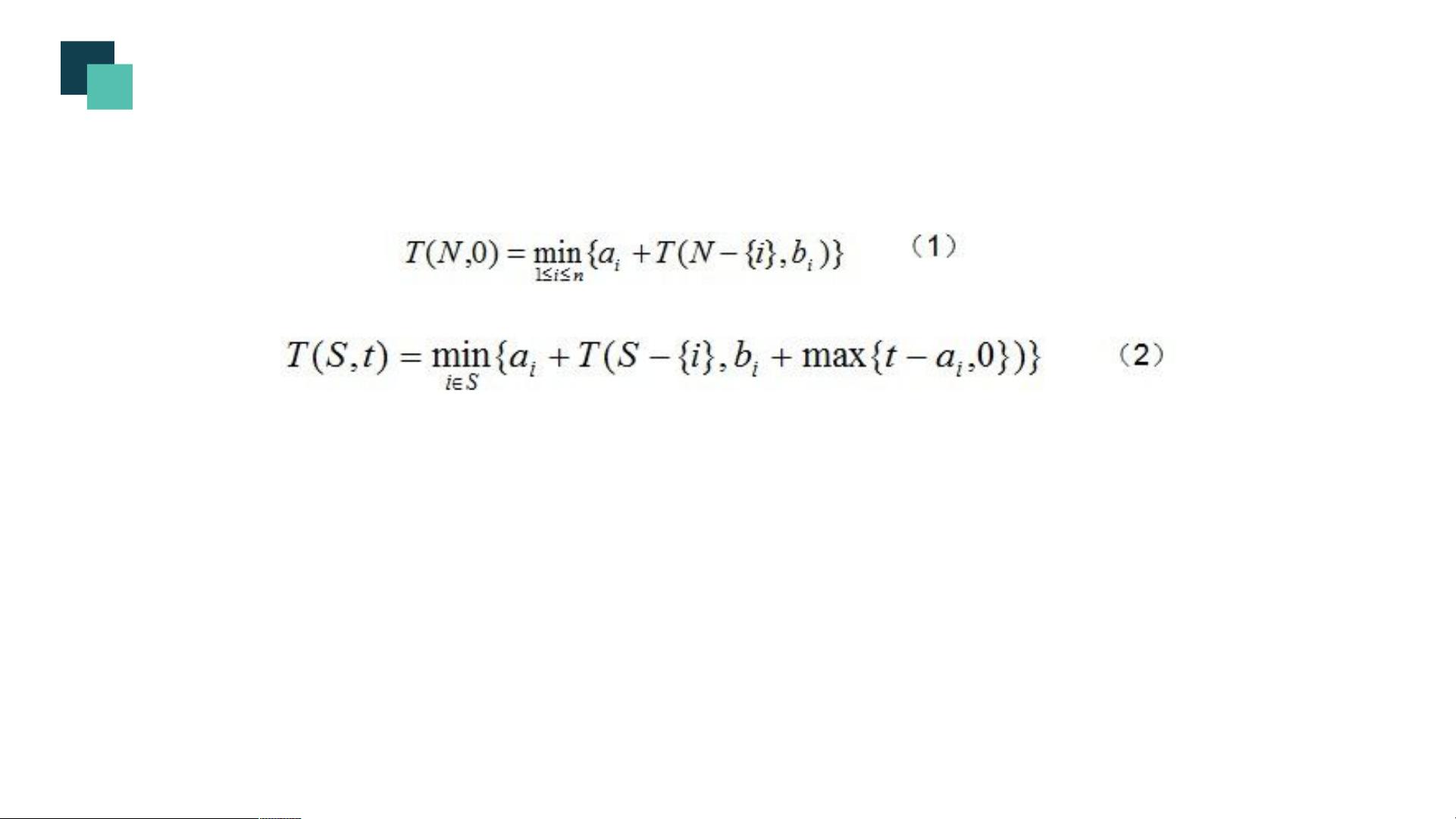流水作业调度算法解析与优化

"这篇PPT主要讲解了流水作业调度问题，包括算法的设计和分析，重点关注如何最小化从第一个作业开始到所有作业在第二台机器上完成的总时间。" 在计算机科学和运营研究中，流水作业调度是一个重要的问题，尤其在优化生产效率和资源利用率的场景中。该问题描述了n个作业需要在由两台机器M1和M2组成的流水线上进行加工，每个作业先在M1上加工，然后在M2上加工，目标是最小化整个流程的总完成时间。 根据描述，一个直观的最优策略是使得M1没有空闲时间，并尽量减少M2的空闲时间。然而，实际情况中，由于作业的先后顺序和不同作业在两台机器上的加工时间差异，可能会出现M2的作业积压或空闲情况。 为了解决这个问题，PPT引入了最优子结构的概念。设π为一个最优调度，它的加工时间由第一个作业在M1上的时间aπ(1)加上在M2等待bπ(1)时间后，剩余作业π(2)至π(n)的最短完成时间T’组成。如果我们将除第一个作业π(1)外的作业集合S在M2等待bπ(1)时间后的最短完成时间记为T(S,bπ(1))，可以证明T’等于T(S,bπ(1))，即最优调度的子问题也具有最优解。 通过这个最优子结构，我们可以采用动态规划或者回溯搜索的方法来求解。对集合中的每个作业进行尝试，比较不同调度下的总时间，选取最佳的顺序。公式(1)表明问题可以通过递归地解决子问题来逐步缩小规模。而公式(2)则指出，对于作业集S的调度，M2的等待时间取决于M1的完成时间和可能的负等待时间的调整，取两者之间的最大值。 例如，如果有三个作业，我们需要考虑所有可能的顺序，计算它们的总时间并选择最短的。对于四个或更多的作业，这样的组合会更多，需要更复杂的算法来处理。 流水作业调度问题是一个典型的组合优化问题，涉及到排序和调度策略的选择。解决这类问题通常需要深入理解作业间的依赖关系、机器的处理能力以及优化目标。在这个PPT中，通过实例和理论分析，深入探讨了如何设计和分析这类问题的解决方案。