数据结构讲解：栈与队列的应用及实现

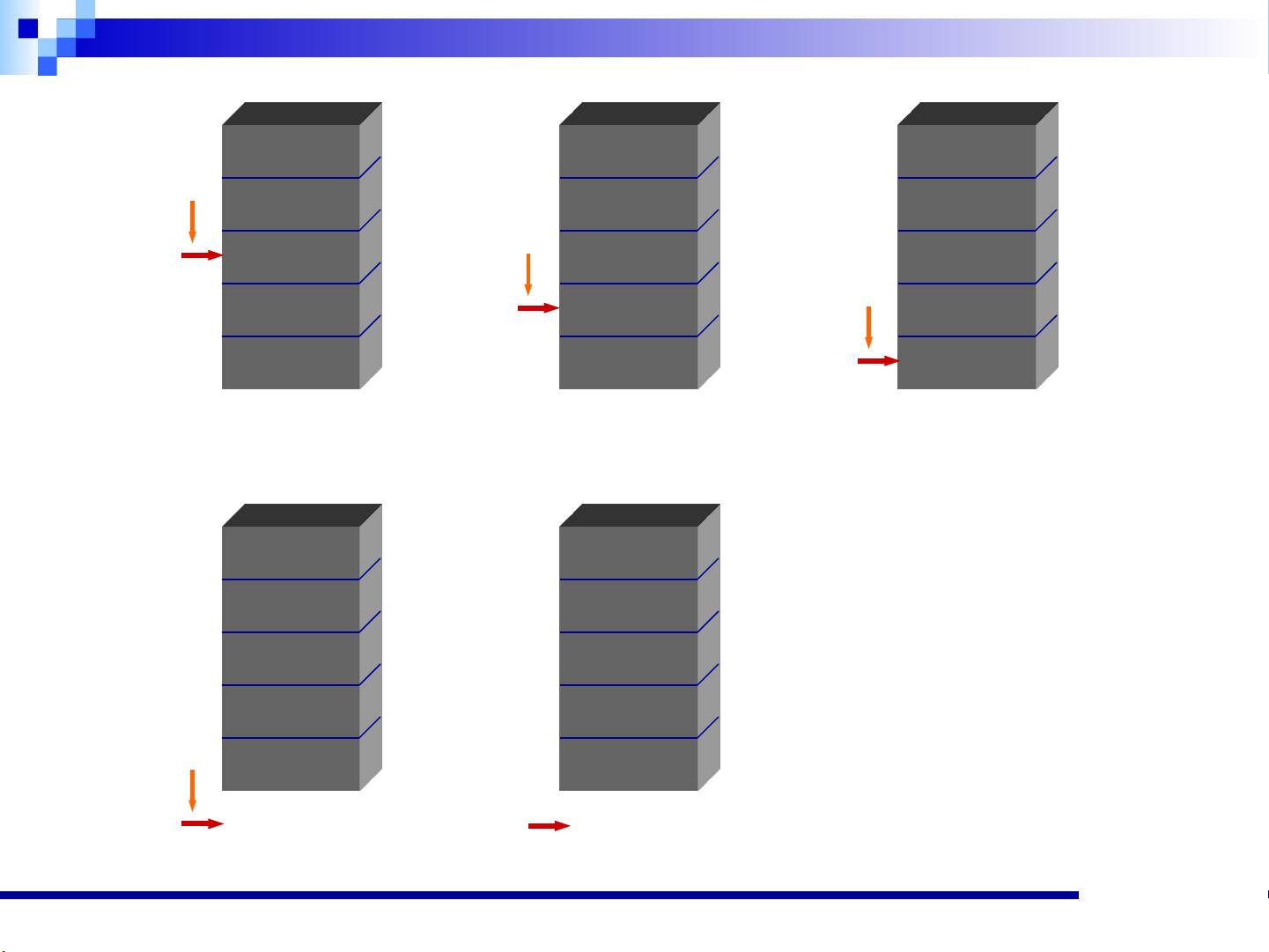
"第三章 栈与队列的讲解，包括栈和队列的基本概念、应用实例以及相关数据结构的设计" 栈（Stack）是一种特殊的数据结构，它遵循后进先出（Last In First Out，简称LIFO）的原则。在栈中，元素的添加和删除都发生在同一端，即栈顶。栈的这种特性使得它在处理需要顺序逆序处理的问题时非常有用，例如在表达式求值和递归调用中。 1. 表达式求值：在计算数学或计算机科学中的表达式时，通常使用后缀表达式（也叫逆波兰表示法）。栈在这里用于存储运算符和操作数，每当遇到一个运算符时，就从栈中弹出两个操作数进行运算，并将结果压入栈中，直到表达式结束。 2. 递归：函数的递归调用实质上是利用了栈来保存每次调用的状态（包括局部变量和返回地址）。当函数调用自身时，新的调用信息会被压入栈顶，而之前的调用信息则留在栈底。直到所有子调用完成，栈才会逐一恢复到原始状态，实现递归的返回。 队列（Queue）则是另一种线性数据结构，它遵循先进先出（First In First Out，简称FIFO）的原则。队列的一端用于元素的添加（入队），另一端用于元素的删除（出队）。队列在处理需要按顺序处理的问题时非常有效，如任务调度和打印杨辉三角形。 3. 打印杨辉三角形：杨辉三角形的每一行的元素可以通过维护一个队列来动态生成。每一行的起始和结束元素为1，中间的元素是其上一行相邻两个元素的和。通过队列可以方便地管理当前行的元素，依次出队并计算下一行的元素。 4. 优先级队列（Priority Queue）：优先级队列是一种特殊的队列，其中元素根据某种优先级排序。当删除元素时，不是按照FIFO原则，而是优先删除优先级最高的元素。优先级队列常用于事件驱动的系统和图的最短路径算法（如Dijkstra算法）。 在C++中，我们可以使用模板类`Stack`来定义栈的抽象数据类型，该类包含构造函数、进栈（Push）、出栈（Pop）、获取栈顶元素（getTop）、判断栈是否为空（IsEmpty）和判断栈是否已满（IsFull）等基本操作。实际编程中，栈可以由数组或链表等数据结构实现。 栈和队列是数据结构的基础，广泛应用于计算机科学的各个领域，如操作系统、编译原理、算法设计等。理解它们的工作原理和应用场景对于深入学习计算机科学至关重要。