马建详解：锥形束CT FDK重建算法及其实现原理

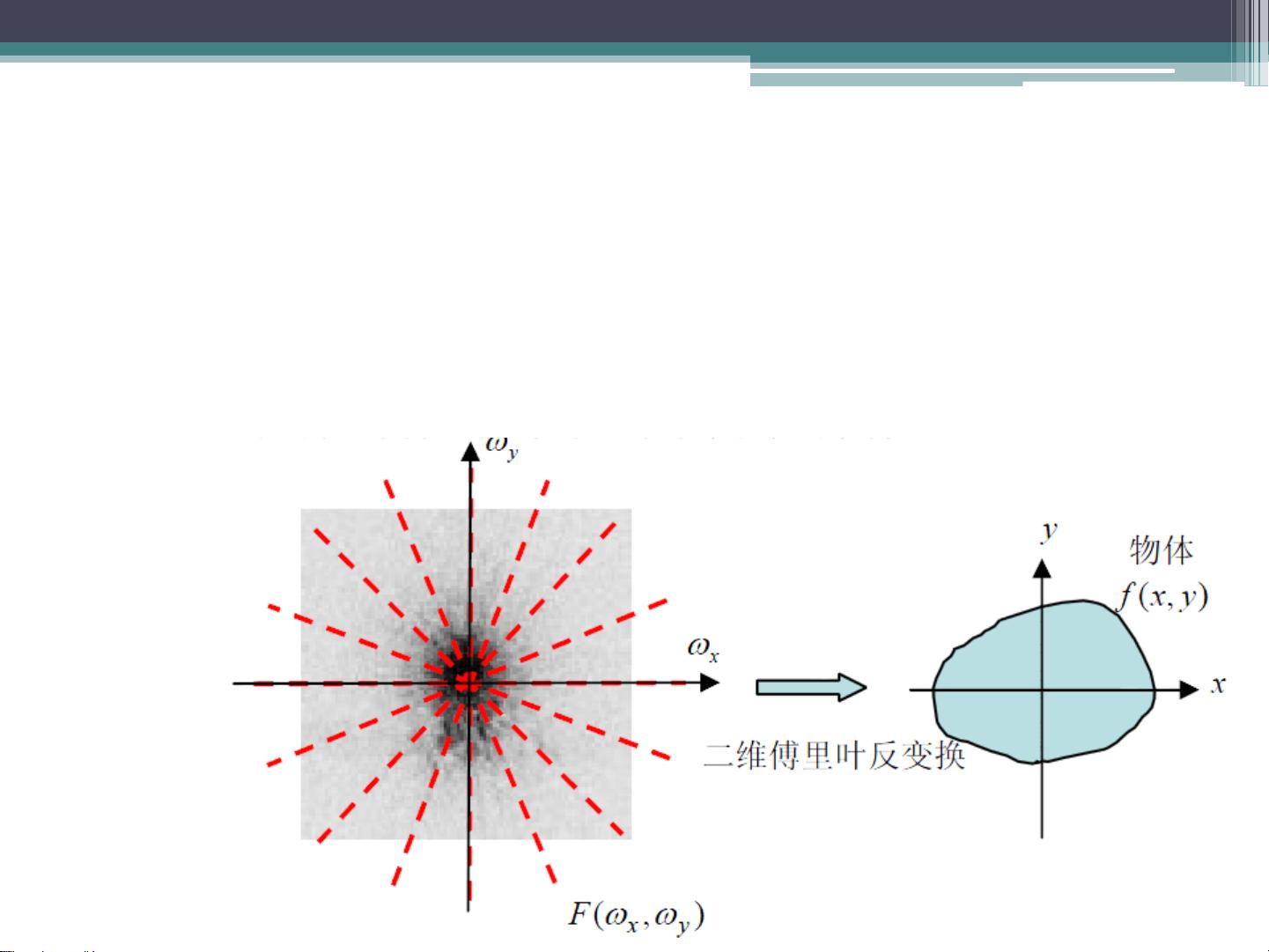
"CT算法重建是医学影像学中的关键技术，尤其在计算机断层扫描（Computed Tomography, CT）领域起着至关重要的作用。马建的《ct-算法重建-马建-fdk重建算法.pdf》文档深入探讨了CT锥形束FDK重建算法，该算法主要针对三维图像的重建，其核心概念包括： 1. 二维与三维重建： - 二维重建主要基于中心切片定理，如平行束FBP（Filtered Backprojection）算法，通过二维线积分投影成像，将探测器收集的投影数据通过傅里叶变换转化为图像。 - 三维重建则是三维锥形束CT的优势所在，FDK算法在此领域尤为突出，它能利用三维线积分投影成像的中心切片定理，通过对多个测量平面的处理获取完整傅里叶空间数据。 2. 锥形束与扇形束重建： - 平行束和扇形束是两种不同的射线分布方式，平行束FBP算法适用于这两种情况，而锥形束FDK算法则通过模拟扇形束的重建过程，解决锥形束聚焦问题。 3. FDK算法详解： - FDK算法最初由Feldkamp, Davis, 和 Kress三人提出，专为处理圆形焦点轨迹的锥形束设计。它的基本思路是将复杂问题简化为扇形束重建，通过一系列步骤，如加权预处理、一维斜坡滤波和锥形束加权反投影，实现精确的图像重建。 4. 三维重建条件： - 三维图像重建需要满足精确重建的条件，如Tuy条件，即每个与物体相交的平面必须包含至少一个焦点。实际采集过程中，使用螺旋轨道、圆圈加直线轨道等轨迹可以满足这一条件。 5. 算法优化： - 为了提高计算效率，文献还讨论了如何利用CUDA（Compute Unified Device Architecture）加速技术，将部分计算任务转移到GPU上，以提升图像重建的速度。 《ct-算法重建-马建-fdk重建算法.pdf》提供了一个全面的框架，详细介绍了CT算法中锥形束FDK重建的核心原理、步骤以及其实现策略，对于理解CT技术的高级应用和技术发展具有很高的参考价值。"