MATLAB实现傅里叶变换详解

"matlab实现傅里叶变换" 在数学和信号处理领域，傅里叶变换是一种将信号或函数从时域表示转换到频域表示的重要工具。MATLAB作为一个强大的数值计算平台，提供了丰富的函数和工具箱来实现傅里叶变换。本资料详细介绍了如何在MATLAB中进行傅里叶变换，并涵盖了多种相关的函数和概念。 首先，资料提到了几种常用的函数，包括阶跃函数、符号函数、矩形函数等。阶跃函数在0点处从0突然跃升到1，MATLAB中用`step`函数来表示；符号函数`sgn`则返回输入值的符号，正数返回1，负数返回-1，零返回0。矩形函数（也称为单位脉冲函数）在一定区间内为1，其余为0，MATLAB通常用`rect`函数来表示。 卷积是傅里叶变换中的一个重要概念，它描述了两个函数的乘积在频域上的表现。卷积在信号处理中用于合并、滤波和分析信号。在MATLAB中，可以使用`conv`函数实现卷积。 傅里叶变换的定义是将一个时间域或空间域的函数映射到频率域。MATLAB中的`fft`函数可以用来执行离散傅里叶变换（DFT），而`ifft`则是其逆运算。对于连续傅里叶变换，MATLAB没有内置函数，但可以通过数值积分的方法近似实现。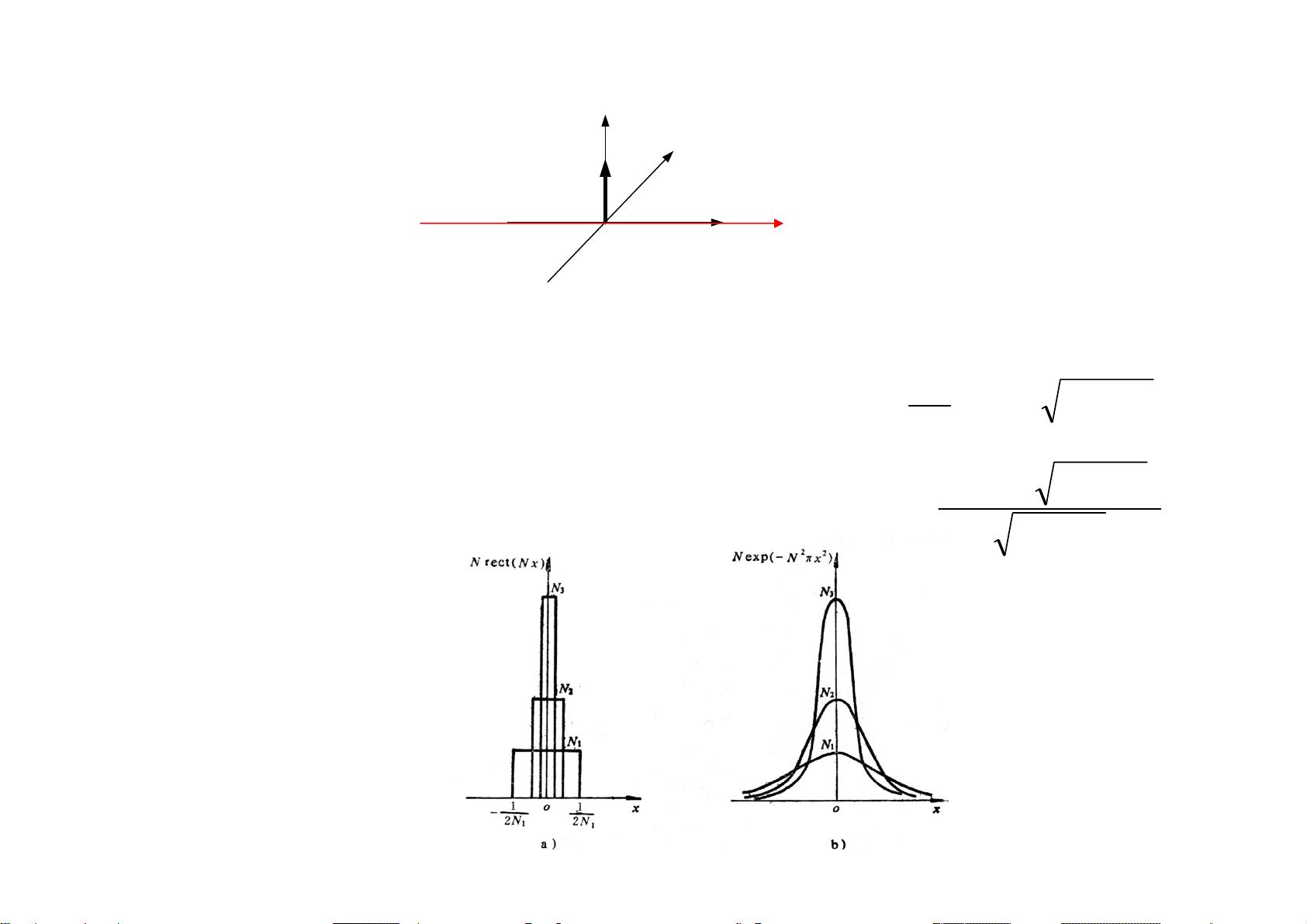 对于不同类型的函数，如阶跃函数、符号函数、矩形函数、高斯函数等，它们的傅里叶变换具有特定的形式。例如，矩形函数的傅里叶变换是Sinc函数。MATLAB可以方便地计算这些函数的傅里叶变换，从而帮助理解信号在频域的特性。 此外，资料还讨论了空间频率的概念，这是图像处理中的关键点，因为它与图像的细节和分辨率有关。傅里叶变换对于图像分析特别有用，可以揭示图像的高频和低频成分。 在MATLAB中实现傅里叶变换的数值计算，通常涉及到离散傅里叶变换的快速算法——快速傅里叶变换（FFT）。`fft`函数在处理有限长度的离散序列时非常高效，它通过复数运算快速计算出DFT。 这个资源提供了深入理解傅里叶变换及其在MATLAB中实现的详细教程。从基本的函数定义到复杂的变换理论，再到实际的MATLAB代码，都覆盖得相当全面。对于学习信号处理、图像分析或任何需要频域分析的MATLAB用户来说，这是一个宝贵的参考资料。