Nf=2+1 lattice QCD下的π-π散射相移研究：I=1和I=2波分析

81 浏览量更新于2024-07-16 收藏 1.31MB PDF 举报

本文主要探讨了基于量子色动力学（Quantum Chromodynamics, QCD）的第一原则计算，即在晶格QCD框架下的I=1和I=2π-π散射相移。这项研究使用了一个特殊的计算配置，即包含Nf=2+1个异构动力学性质的轨距场，采用的是改良的三叶草型威尔逊费米子（Clover-improved Wilson fermions）。这种费米子处理方法在保证理论精确性的前提下，有助于减少计算中的系统误差。研究者们使用了一个大型的空间体积V = (3.7 fm)^3，这样的设置对于提高能量分辨率至关重要，因为更大的体积意味着更精细的尺度分辨率，有助于更准确地捕捉到散射过程中的细节。选择的介子质量mπ = 230 MeV，这是一个重要的参数，因为它直接影响着强相互作用力的表现和理论预测的可靠性。在计算过程中，随机LapH方法被有效地应用于计算时间相关矩阵，这是克服大规模晶格QCD计算中复杂性的重要手段。相比于以往的工作，这个方法显著提高了计算效率，使得在如此大体积下进行高精度模拟成为可能。结果显示，对于I=2s波，研究人员得到了清晰的信号，得到了相应的物理参数m / m = 3.350（24）和g = 5.99（26），这些数据对于理解π-π散射的性质以及检验QCD理论预测具有重要意义。这项工作的成功不仅展示了随机LapH方法在大体积计算中的实用性，也为未来的研究奠定了基础，即利用最新计算资源研究晶格间距效应以及散射振幅对夸克质量依赖性的定量分析。它标志着量子色动力学在解决复杂强相互作用问题上取得了实质性的进展，并且对于粒子物理学的理论发展和实验验证具有重要的指导价值。这项成果已经开放存取，可在《核物理学B》(Nuclear Physics B) 910期（2016年）的842-867页找到，可以通过Elsevier网站（www.elsevier.com/locate/nuclphysb）访问。编辑为本研究提供了关键的支持和审阅，由Hong-Jian He担任。

846 J. Bulava et al. / Nuclear Physics B 910 (2016) 842–867

evident in the measured correlation functions.

In order to mitigate effects of this autocorrelation

on estimates of statistical uncertainties, we average measurements on pairs of subsequent con-

ﬁgurations. Statistical errors are estimated using the bootstrap technique [26] on this rebinned

ensemble with N

=800 bootstrap samples.

In this anisotropic setup the lattice re

gulator is fully speciﬁed by the temporal lattice spacing

and renormalized anisotropy ξ = a

. The anisotropy is determined from the (continuum)

pion dispersion relation



)



=(a

)



2πa

ξL



, (2.1)

where d ∈Z

is the quantized ﬁnite-volume three-momentum of the pion.

Determination of ξ requires the single-pion ener

gies a

) in Eq. (2.1). Periodic tempo-

ral boundary conditions are used for this ensemble, potentially complicating the extraction of

ﬁnite-volume energies from the fall-off of temporal correlation functions. In particular, a sin-

gle zero-momentum pion correlation function has the ‘cosh’ form in the limit of ground-state

saturation

lim

t1/E

T −t 1/E

(t) = Ae

−m



1 + e

−m

(T −2t)



, (2.2)

where E

is the relevant ﬁrst excited-state energy. Two-pion correlation functions with zero total

momentum have the more complicated form (ignoring small energy shifts due to pion interac-

tions)

lim

t1/E

T −t 1/E

2π

(t) = Ae

−2m



1 + e

−2m

(T −2t)

+Be

−m

(T −2t)



, (2.3)

while two-pion correlation functions with non-zero total momenta have a similar but more com-

plicated additional exponential term.

Since our ﬁnite-v

olume energies are extracted from ﬁts of temporal correlation functions to

an exponential form, these additional terms add potentially signiﬁcant complication as has been

discussed in (e.g.) Ref. [9]. Fortunately, the large temporal extent of our lattice (m

T ≈ 10) sup-

presses such terms below the statistical accuracy of the energy levels. This can be demonstrated

by performing two-parameter correlated-χ

ﬁts of the single zero-momentum pion correlation

function to both a single exponential and the cosh of Eq. (2.2). The second exponential in

Eq. (2.2) is larger than or equal to the additional problematic exponential terms which appear

in two-pion correlation functions, apart from small hadronic interaction effects.

As the single pion at rest is our most precisely determined correlation function, it is most

sensiti

ve to these thermal effects. The absence of these effects, such as the second exponential

in Eq. (2.2), indicates that additional exponentials in two-pion correlation functions may be ne-

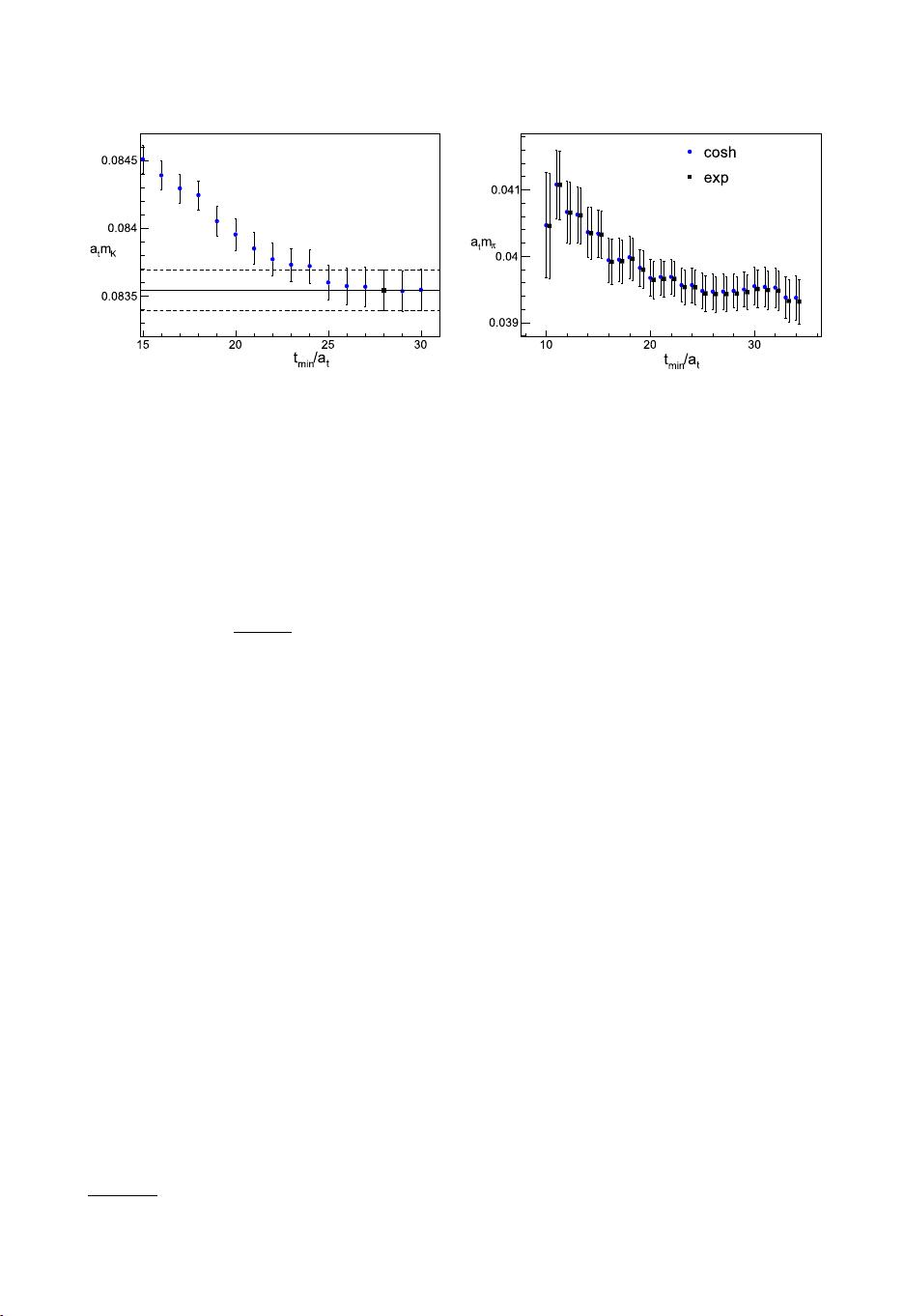
glected. The comparison of single-exponential and cosh ﬁts for v

arious ﬁtting ranges is shown

in Fig. 1. Clearly, no effect from the ﬁnite temporal extent is evident for these temporal separa-

tions. All subsequent correlated-χ

ﬁts to temporal correlation functions will thus ignore ﬁnite-T

effects. The extraction of these energies will be discussed in more detail in Sec. 2.3.

The ﬁts to the single-pion zero-momentum correlation function sho

wn in Fig. 1, as well as all

other ﬁts to correlated data in this work, minimize a correlated-χ

to properly treat the covariance

In lattice QCD the largest autocorrelations are typically observed for ‘smoothed’ observables such as the topological

charge and smoothed action [25], which are not examined here.

J. Bulava et al. / Nuclear Physics B 910 (2016) 842–867 847

Fig. 1. Left: t

min

-plot (deﬁned in the text) for two-parameter single-exponential correlated-χ

ﬁts used in the determina-

tion

of a

from which a

is set. The solid and dashed lines show the mean value and 1σ errors (respectively) for the

chosen ﬁt range, which is also indicated by a black square. Right: Comparison of t

min

-plots for single-exponential ﬁts

(denoted ‘exp’) and cosh ﬁts according to Eq. (2.2) for the single-pion correlation function with zero total momentum.

Fit ranges are shown with t

max

= 38a

and varying t

min

. The consistency of these two ﬁt forms for our most precisely

determined correlation function demonstrates that ‘thermal’ effects due to the ﬁnite temporal extent may be neglected.

between observables measured on the same ensemble of gauge conﬁgurations. The covariance

matrix is obtained using the bootstrap estimator

Cov(t, t



) =

−1



n=1

(C(t)

−C(t))(C(t



)

−C(t



)), (2.4)

where N

= 800 is the number of bootstrap samples, C(t)

is the bootstrap replicum of C(t)

on the nth sample, and C(t) is the average over all bootstrap replica. The covariance matrix

is taken as identical across each bootstrap sample’s determination of the ﬁt parameters.

Apart from ef

fects due to the ﬁnite temporal extent, the range of timeslices [t

min

, t

max

] over

which the ﬁt is performed is another source of systematic error. In particular, ﬁtted values exhibit

a marked sensitivity to t

min

due to the inﬂuence of higher-lying exponentials in Eq. (1.1). In this

work we employ ‘t

min

-plots’ to ensure that this systematic error is smaller than the statistical er-

ror on the ﬁt parameters. The guidelines for selecting a t

min

satisfying this criterion are given in

Eq. (2.11). These plots show the ﬁtted values for many t

min

with a ﬁxed t

max

, and are exempliﬁed

in Fig. 1 which shows t

min

-plots for a

and a

. With stochastically-estimated correlation

functions, t

min

-plots are preferable to effective masses m

eff

(t) = ln[C(t)/C(t + 1)] for deter-

mining the range of times over which a single exponential dominates. Stochastically-estimated

effective masses typically have larger error than the corresponding ﬁtted energies and are thus

not useful to assess systematic errors from the choice of t

min

We no

w discuss two determinations of ξ . In the ﬁrst, single-pion energies at various total mo-

menta

are ﬁrst obtained from this ﬁtting procedure and then used in Eq. (2.1). The t

min

-plots

for single-exponential ﬁts to these correlation functions together with the ﬁtted energies used in

our analysis are given in Fig. 8 of Appendix A. Generally, these energies are chosen somewhat

conservatively so that systematic errors due to excited-state contamination are small in com-

parison to the statistical errors. They are summarized in Fig. 2 together with a ﬁt to Eq. (2.1)

for d

≤ 6. Correlation exists among the ﬁtted energies; their covariance is estimated using the

Pion correlation functions are averaged over equivalent momenta before ﬁtting.

剩余25页未读，继续阅读

weixin_38522636

粉丝: 3
资源: 913

Nf=2+1 lattice QCD下的π-π散射相移研究：I=1和I=2波分析

从LaAL涂片的HAL QCD方法得到的I = 2ππ散射相移

N f = 2 +1 + 1晶格QCD的强子-强子相互作用：isospin-2ππ散射长度

Nf = 2 + 1 + 1晶格QCD的强子-强子相互作用：I = 3/2πK散射长度

从= 2 +1格QCD得出的= 1 Pion–pion散射幅度和时态Pion形状因数

从晶格QCD提取等量ππ相移

从晶格QCD得到的I = 3三点散射振幅

η→3π和ππ散射对低能QCD参数的约束

QCD的弹性πK散射的夸克质量相关性

K→ππ衰变中的最终状态相互作用：ΔI= 1/2规则与ε'/ε

国家自然科学基金（11775165）和中央高校基础研究基金资助，pion超流体中的夸克-反夸克散射相移和介子谱函数

最新资源