2013级计算机图形学A卷试题解答：平行线与垂直线变换特性

本篇文档是关于计算机图形学的一份期末考试试卷A卷，主要考察了学生对3D向量表示、辐射度方法、四元数旋转、投影类型以及线性变换的理解。以下是关键知识点的详细解析： 1. **3D向量的homogenized坐标表示**: 在三维空间中，使用homogenized坐标（也称为归一化设备坐标或齐次坐标）来表示向量时，第四个坐标（通常记为w）被设置为1，使得点（x, y, z, w）可以用来表示一个在空间中的位置。这个坐标系统对于线性变换特别有用，因为它们保持了向量的方向关系。 2. **辐射度方法（Radiosity Method）**: 这种方法基于假设场景中的所有表面都像扩散反射器一样工作。它通过考虑每个像素如何接收和重新发射光线来模拟光照，试图达到全局照明的真实效果。核心思想是通过迭代计算物体之间的能量交换来模拟自然光的行为。 3. **四元数（Quaternions）**: 四元数是一种用于表示三维旋转的数学工具，它扩展了复数的概念到四维空间。相比于传统的旋转矩阵，四元数更高效且避免了 gimbal lock（旋转轴锁定）问题，特别是在连续旋转和动画应用中非常常见。 4. **投影类型：平行投影与透视投影**: 平行投影是一种特殊的透视投影，其中观察者位于无穷远，这使得所有的平行线在图像上仍然保持平行。而一般透视投影则会根据距离的改变使平行线在视平面上收敛。 5. **曲线的参数连续性**: 当两条曲线段在某一点相接，且它们都以相同的导数接近该点时，我们说这种连接是参数连续的。这意味着在局部平滑地转变曲线上任意两点间的参数值不会引起突然的形状变化。 6. **线性变换的性质**: - **a) 关于平行线的映射**: 是的，如果进行仿射变换，平行线将保持平行。原因是仿射变换保持无穷远处的点不变，因此原线段的交点在变换后仍将是两直线的交点，保持平行性。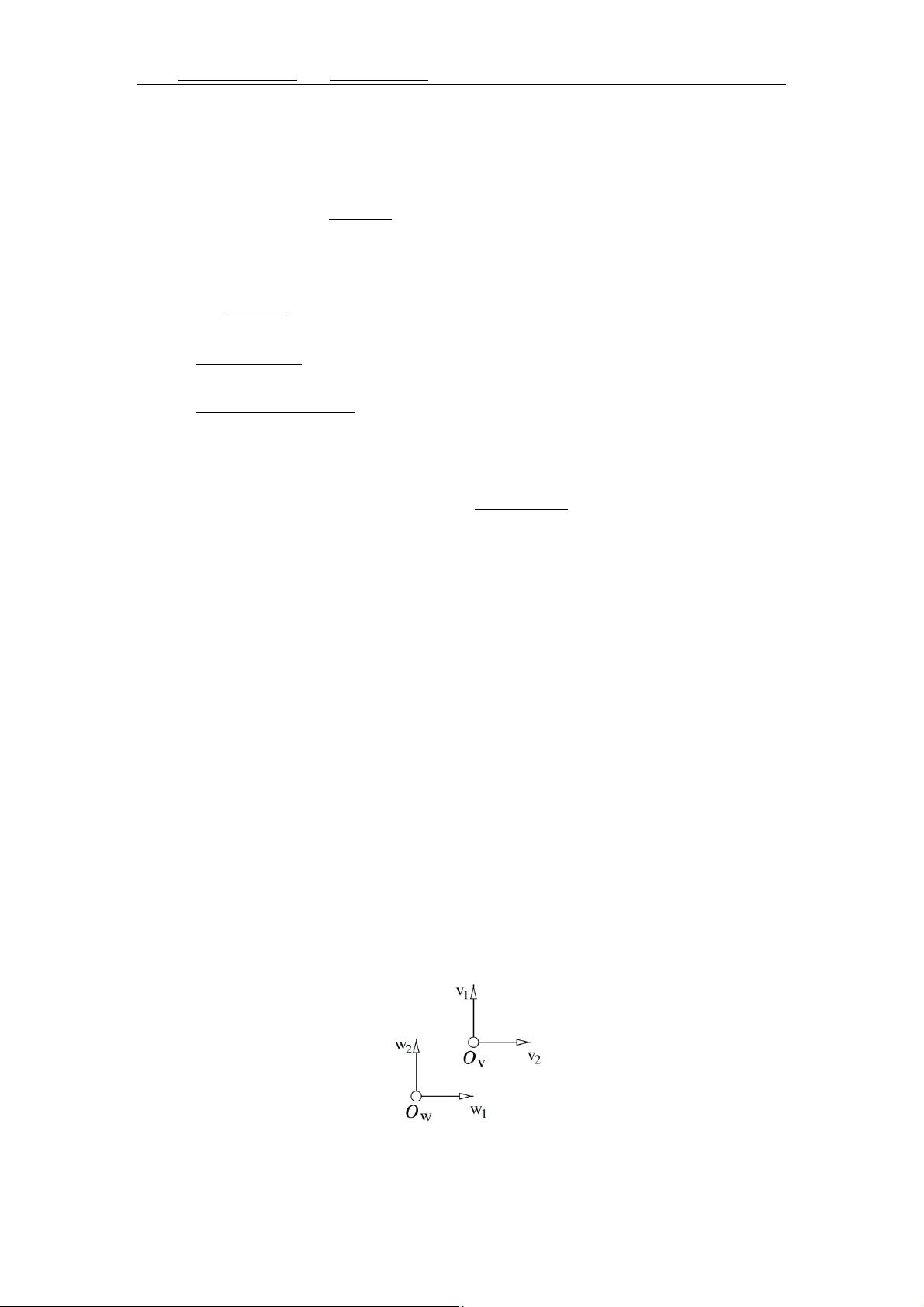 - **b) 关于垂直线的映射**: 否，仿射变换不保证垂直线在映射后仍然垂直。给出的例子可能是为了说明这个情况，比如存在一种特殊情况下的非线性变换可能导致垂直线变倾斜。 这些知识点展示了计算机图形学中基础几何、投影理论和变换原理的应用，对于理解图形渲染、模型处理和视觉效果的实现至关重要。通过解答这些问题，学生可以深化对这些概念的理解，并检验他们在实际应用中的运用能力。