多目标优化与决策：Matlab实现与方法解析

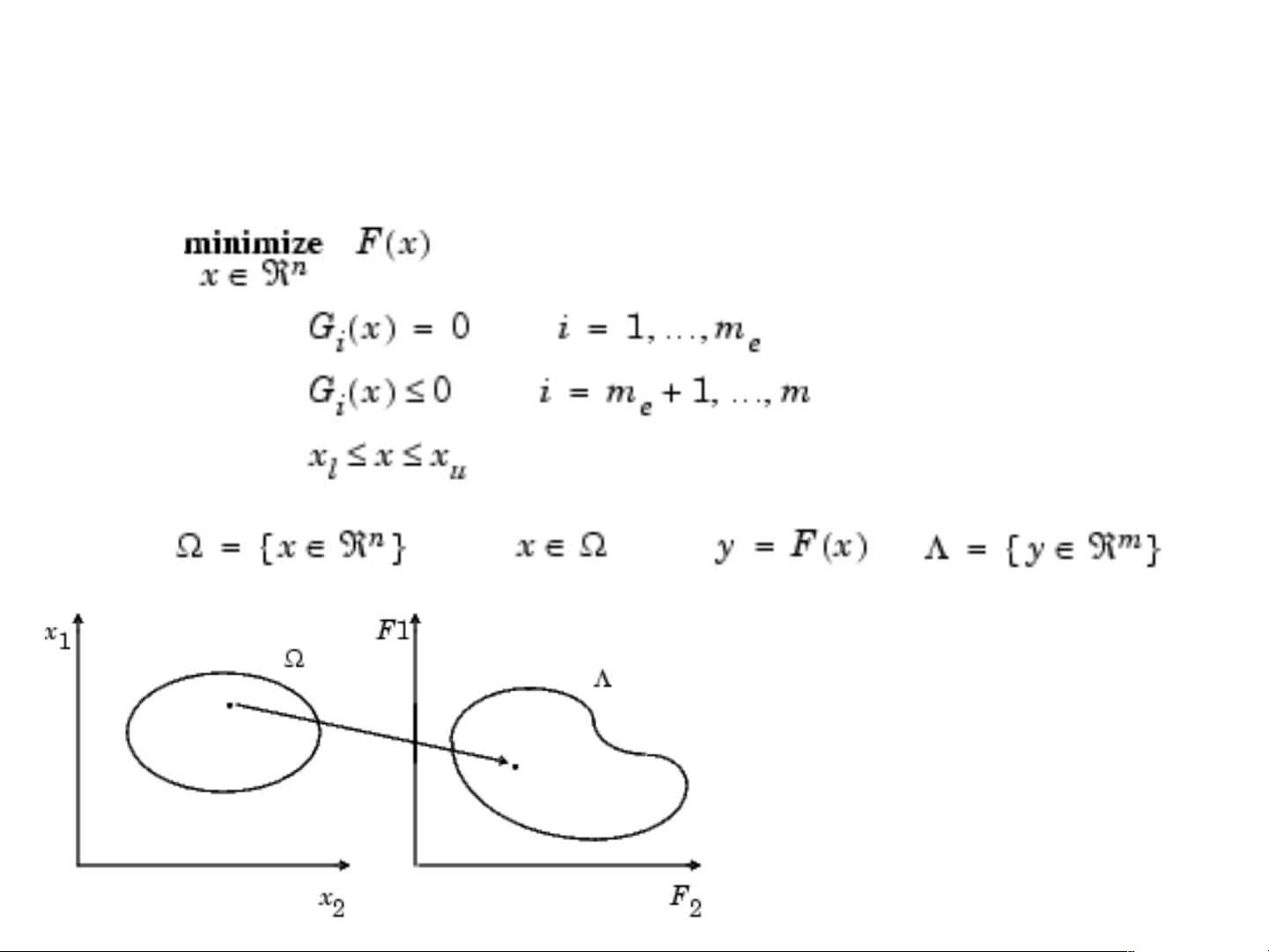
"该资源是关于系统工程概论中的多目标优化与决策的基本方法的介绍，主要探讨了多目标优化问题、约束法和目标规划法，并结合Matlab的Optimization Toolbox进行了讲解。" 多目标优化问题是一种在多个相互冲突的目标之间寻求平衡的优化问题。在数学模型中，它涉及到一个由参数向量 \( x \) 控制的函数集合 \( F \)，这些函数通常被称为目标函数，它们映射到目标函数空间 \( \Omega \)。非劣解集是满足所有目标函数的解集，其中没有其他解可以同时在所有目标上做得更好。在非劣解集中，任何一对解如果不能同时在所有目标上得到改善，则被认为是等效的。 约束法是一种处理多目标优化的方法，它通过选择一个主要目标函数 \( F_p \)，并把其他目标转化为约束条件来实现。这种方法的优点是可以捕获那些加权法可能会遗漏的解，但其缺点也非常明显，如选择合适的松弛度 \( \varepsilon \) 的困难，以及在大规模问题中的高计算复杂度。 目标规划法，或称为fgoalattain函数在Matlab中的应用，是一种更加直接的方法，旨在找到一个非劣解，使其到预设目标 \( F^* \) 的距离最小。这种方法引入了松弛度 \( \gamma \)，通过最小化松弛度来寻找最可行解。目标规划法的优点在于不漏解，目标明确，且计算量相对较小。然而，对于非线性问题，可能只能得到局部最优解，而且在局部搜索时，线性的权值松弛可能导致错过全局优化的机会。 在工程领域，多目标优化尤其重要，因为它经常出现在需要平衡不同性能指标的问题中，如成本、效率和可靠性。Matlab的Optimization Toolbox提供了工具来处理这些问题，如fgoalattain函数，它可以用于目标规划，处理线性和非线性问题，但可能需要根据具体问题调整参数以达到满意的结果。 多目标优化与决策涉及复杂的数学理论和实用策略，包括如何选择目标函数权重、处理约束以及如何利用特定的优化工具，如Matlab的Optimization Toolbox。理解这些基本方法对于解决现实世界中的系统工程问题至关重要。