贪婪算法与最小生成树

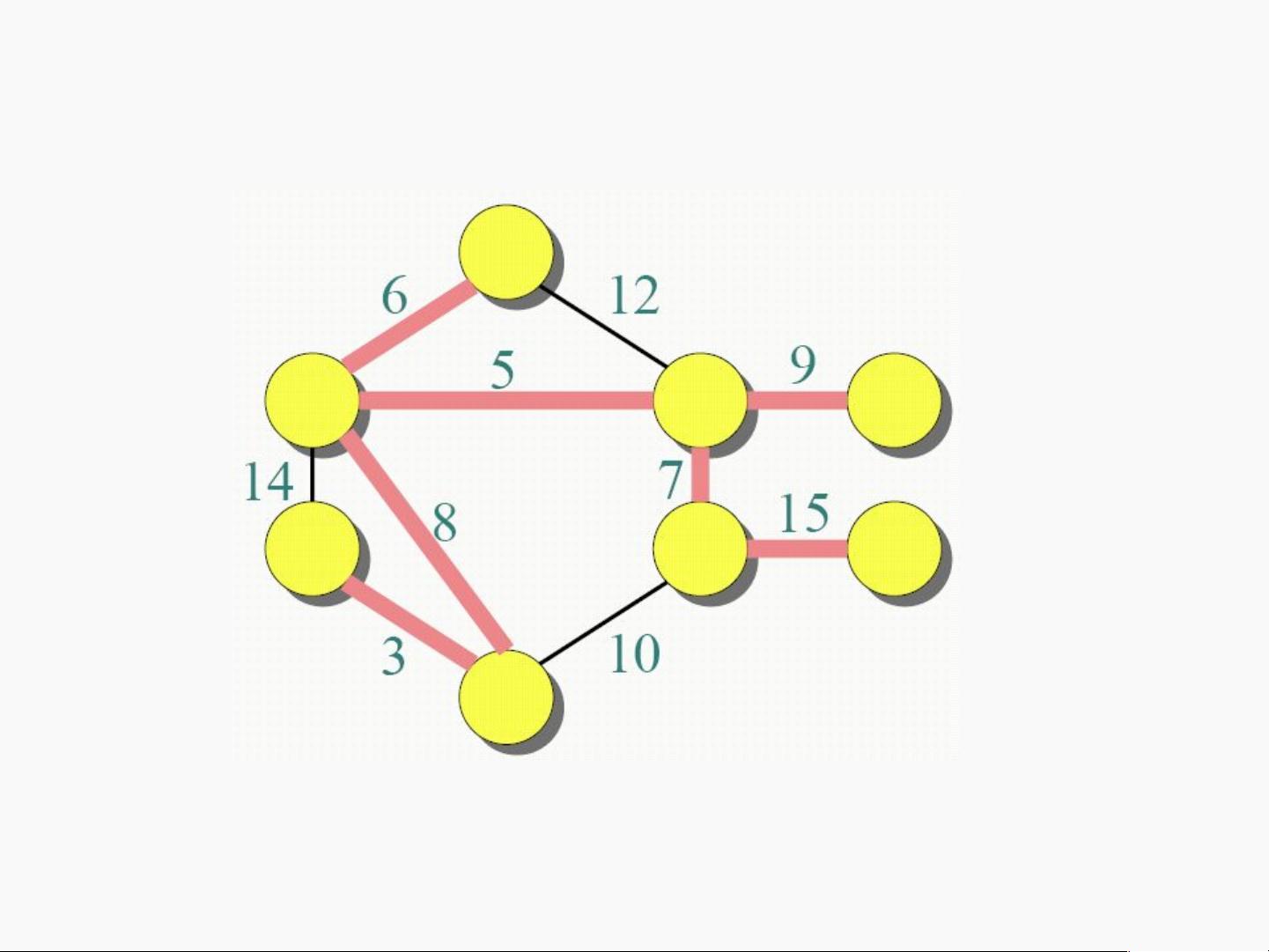
"该资源是一个关于贪心算法的PPT，主要内容涵盖了图的表示方法、最小生成树的概念以及贪心选择策略，特别是介绍了Prim's贪婪最小生成树算法，并讨论了最优子结构在解决此类问题中的应用。" 贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。这种策略通常用于求解最优化问题，但在每一步选择时并不考虑全局最优，只保证当前选择最优。 图的表示主要有两种方法： 1. 邻接矩阵：对于图G=(V,E)，邻接矩阵A是一个二维数组，其中A[i][j]=1表示顶点i和顶点j之间有一条边，否则为0。邻接矩阵适用于稠密图，即边的数量接近于顶点数量的平方，因为它需要O(V^2)的空间。 2. 邻接链表：每个顶点v有一个链表，链表中的元素是与v相邻的顶点。邻接链表对于稀疏图（边的数量远小于顶点数量的平方）更为高效，因为它只需要O(V+E)的空间。 最小扩展树（Minimum Spanning Tree, MST）是图论中的一个重要概念，特别是在加权无向图中寻找一个连接所有顶点且总权重最小的树。这里提到了Prim's算法，它是一种贪心算法，用于构造最小生成树。Prim's算法的基本思想是从一个顶点开始，每次添加一条与当前树中顶点连接且权重最小的边，直到所有顶点都被包含在内。 最优子结构是贪心算法能够成功的一个关键特性，意味着一个问题的最优解可以通过其子问题的最优解来构造。在MST问题中，如果一棵树是另一棵树的子集，并且在原树中是MST，那么这个子树也是其子集的MST。这个性质为动态规划或贪心算法提供了基础。 在Prim's算法中，每次添加的边保证了当前生成树的最优性，但并没有解决重叠子问题，因为每次只考虑一条边的添加。然而，由于MST问题的特殊性，贪心策略可以有效解决问题，而不需要像动态规划那样系统地解决所有子问题。每次选取边时，贪心算法都选择当前未加入树的边中权重最小的一条，这样逐步构建的树保证了总权重最小。 这个PPT深入讲解了贪心算法在解决图论问题，特别是最小生成树问题中的应用，通过邻接矩阵和邻接链表展示了图的不同表示方式，并探讨了最优子结构如何支持贪心策略的有效性。