最小二乘法曲线拟合：龙贝格算法与MATLAB实现

"该资源是一份关于使用最小二乘法进行曲线拟合的实验报告，主要探讨了如何利用龙贝格算法实现这一过程，并在MATLAB环境下编写了源程序。实验目的是通过编程提高工作效率，对给定的一天中不同整点时刻的气温数据进行拟合分析，以确定气温变化规律。实验内容包括使用二次、三次、四次多项式以及特定形式的函数对气温数据进行拟合，并对比分析误差。报告中还详细介绍了最小二乘法的基本原理和算法设计思路，包括求解最小误差平方和的数学公式及其优化过程。" 实验报告详细描述了利用最小二乘法进行曲线拟合的过程，这是一种常用的数据分析方法，用于找到一组离散数据点之间的关系，以便构建连续的数学模型。在这个实验中，学生们被要求使用MATLAB语言实现龙贝格算法，这是一种数值积分的高效方法，也被扩展用于解决最小二乘拟合问题。 实验的焦点是分析某一天内不同时间的气温数据，通过四种不同的函数模型（二次多项式、三次多项式、四次多项式及特定形式的函数）进行拟合。每个模型的目的是找到最能描述气温变化趋势的函数表达式，同时评估它们的误差，通过比较拟合效果选择最佳模型。 最小二乘法的核心是找到使得所有数据点到拟合曲线的垂直距离平方和最小的多项式。数学上，这可以通过最小化误差平方和S来实现，S是各数据点与拟合曲线之间距离的平方和。通过求解这个优化问题，可以得到多项式的系数。实验报告中给出了相关的数学公式和推导，包括梯度为零的必要条件，这是多元函数极值存在的基础。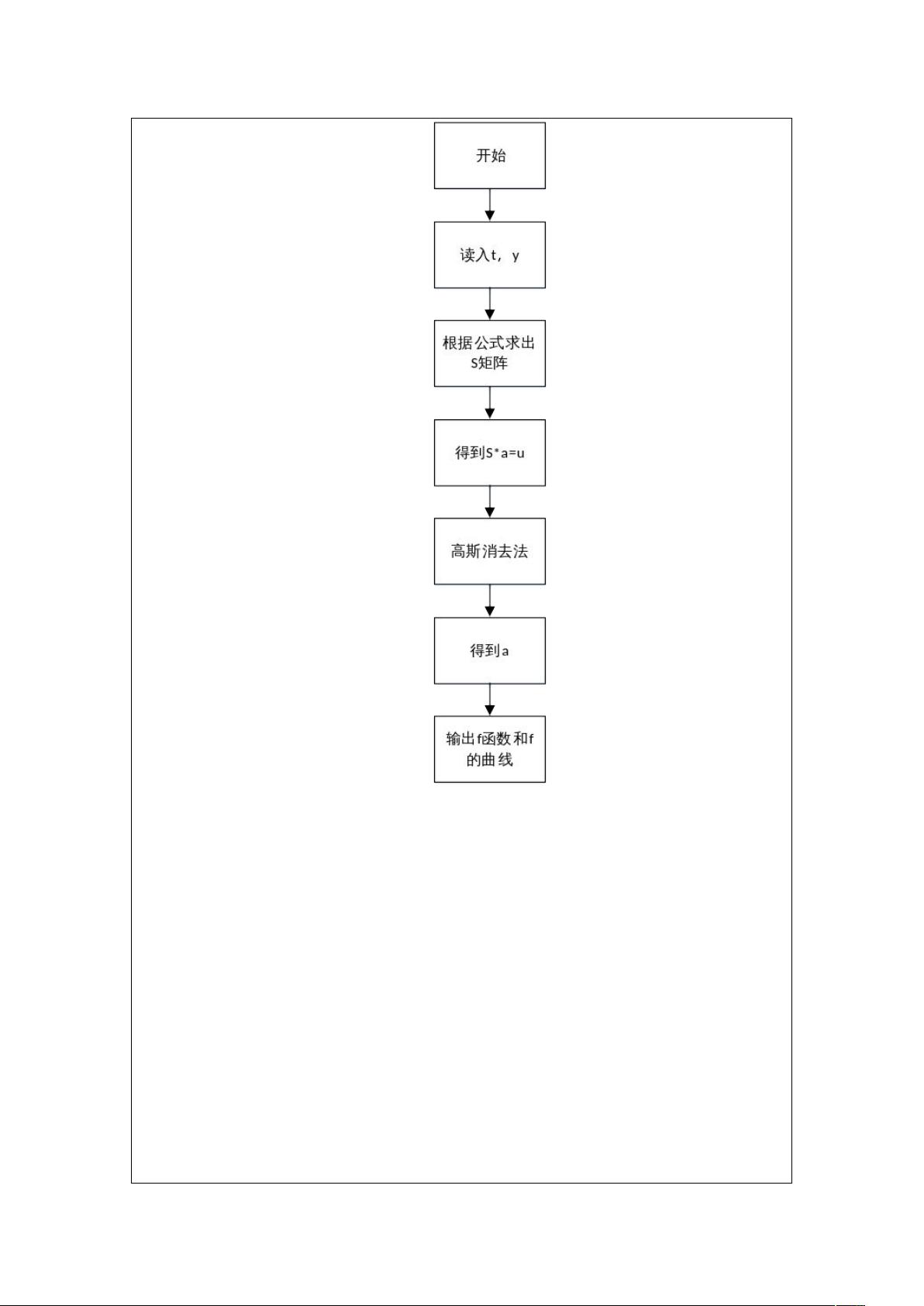 实验方案部分解释了如何运用最小二乘法来拟合多项式。首先，定义一个n次的拟合多项式，然后通过求解线性方程组来确定多项式的系数。这个线性方程组的建立基于误差平方和S的偏导数为零，最后通过龙贝格算法求解这些方程。 这份实验报告提供了一个实践性的学习案例，让学生们能够深入理解最小二乘法和龙贝格算法在实际问题中的应用，同时也展示了MATLAB在数值分析中的强大功能。通过这种方式，学生不仅学习了理论知识，也锻炼了编程和问题解决能力。