分位数回归分析：降水径流变化研究新视角

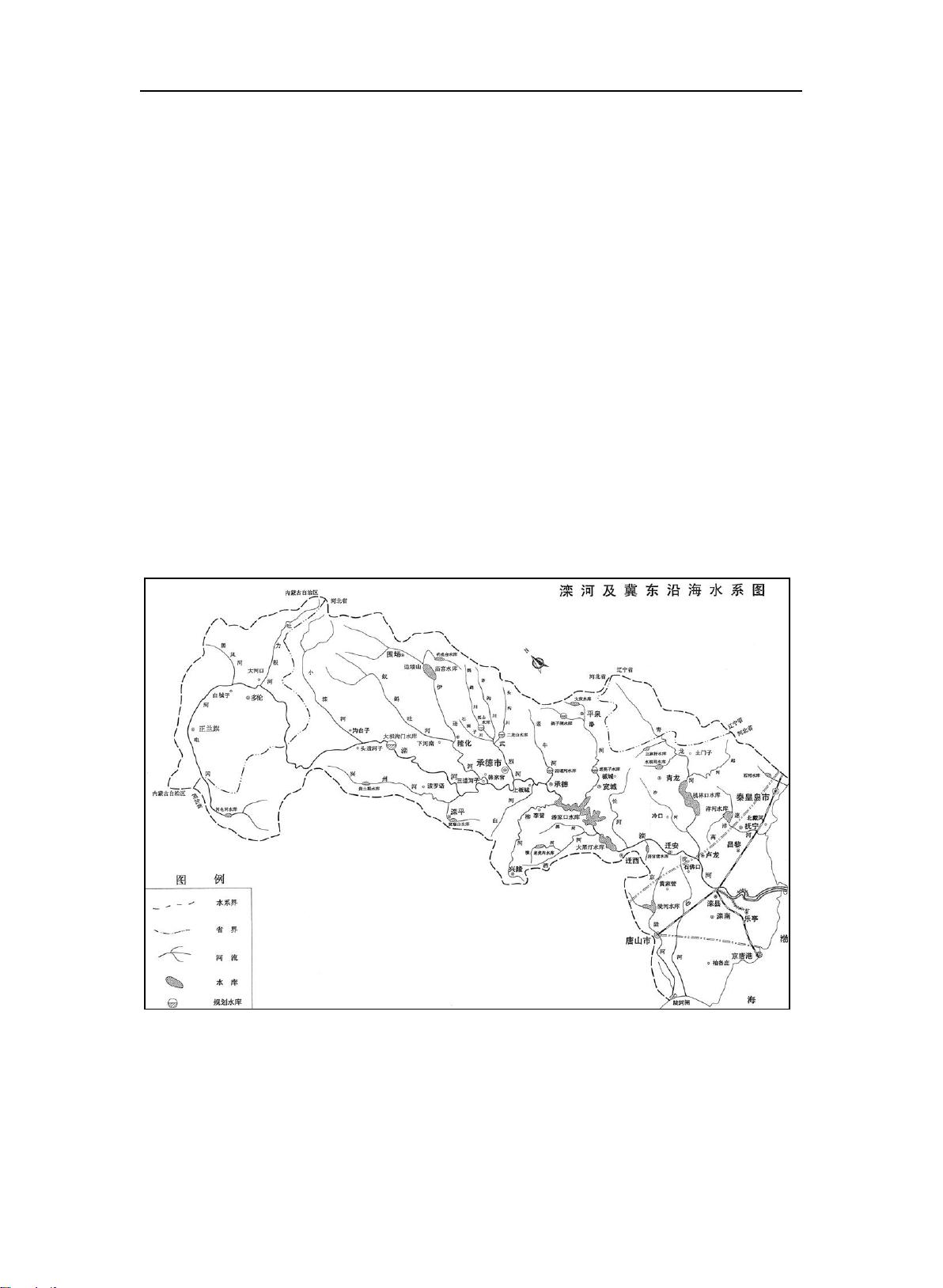
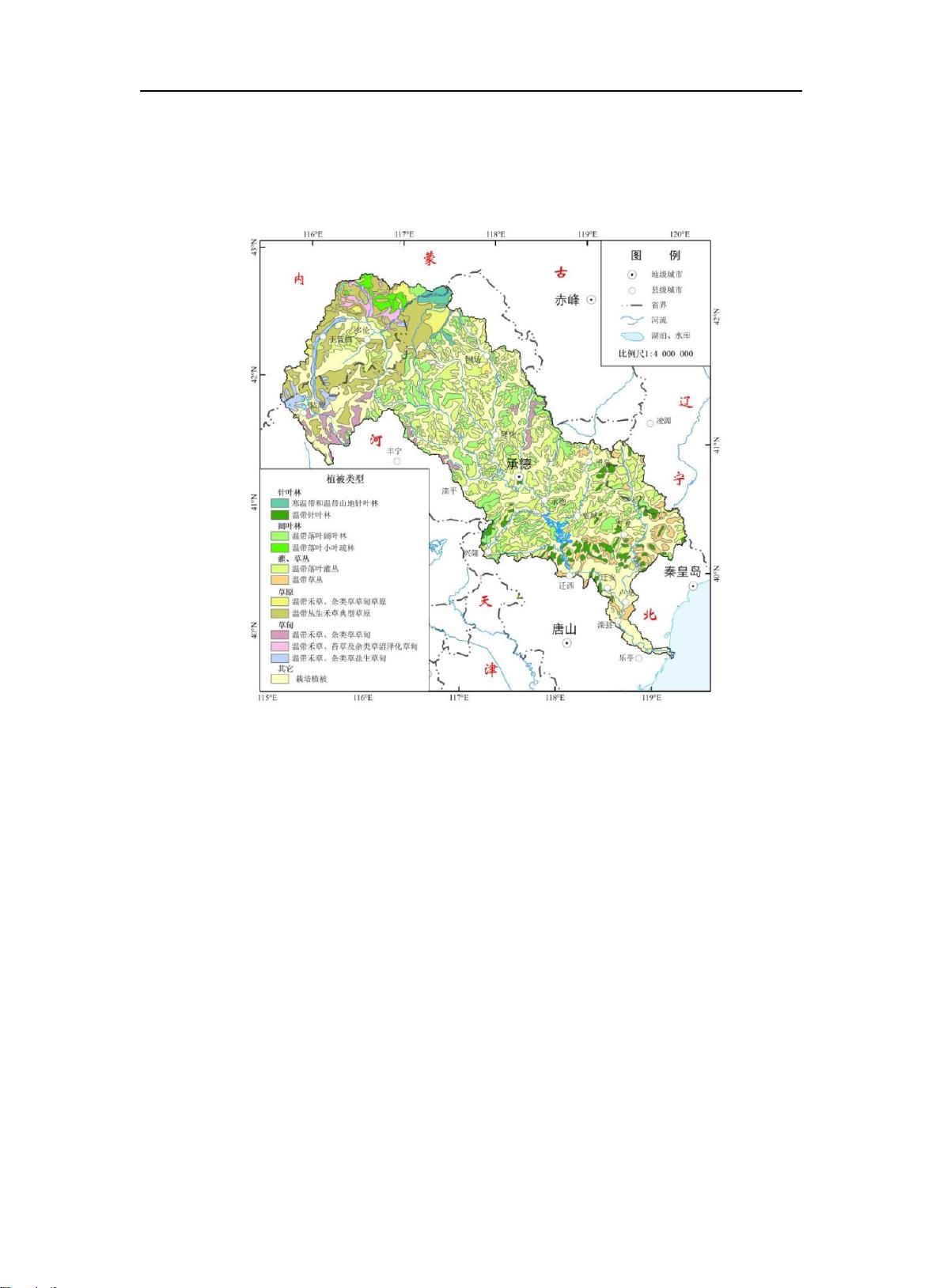
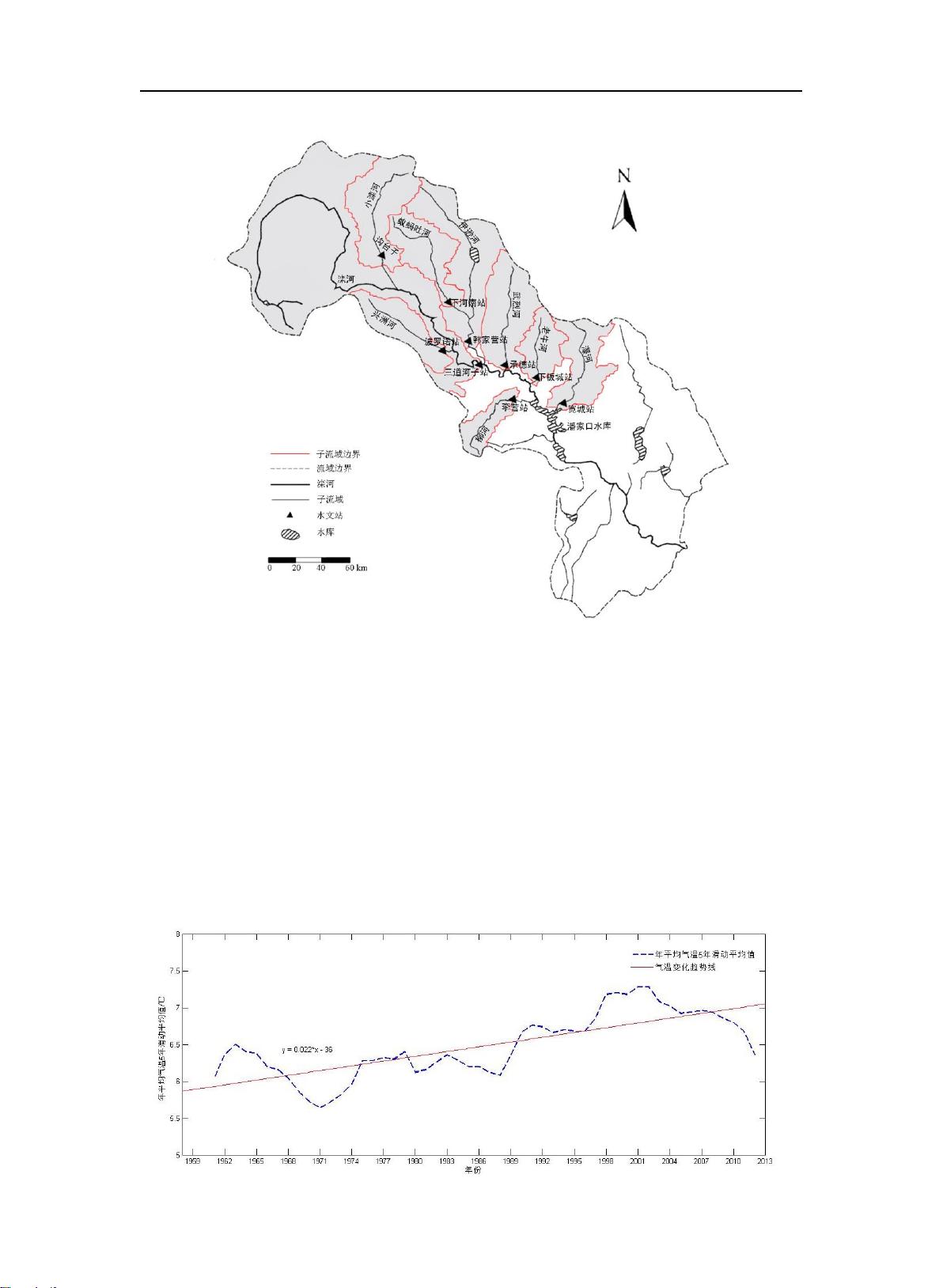
"数据回归-基于分位数回归的降水、径流变化及响应分析" 本文探讨了在气候变化背景下，如何运用分位数回归方法来分析降水和径流系列的变化特性。传统上，学者们利用统计方法、趋势分析和模拟方法等对降水和径流序列进行研究，结果显示这些序列确实在一定程度上发生了变化，尤其是径流序列。在潘家口水库流域，已有许多研究对其降水和径流变化进行了分析，但本文旨在采用一种不同的方法——分位数回归法，以提供新的视角。 分位数回归是一种统计分析技术，虽然在水文学领域的应用相对较少，但在数学、经济学和医学等领域广泛使用。相比其他方法，分位数回归的优势在于其使用条件更为宽松，并且对异常值的干扰具有较强的抵抗力，结果更加稳健且丰富。这种方法的求解过程不依赖于数据的正态分布假设，因此对于非线性关系和异方差性的数据集尤为适用。 在分析降水和径流变化时，分位数回归能够捕捉到整个分布的不同部分（如中位数或更高或更低的分位数）的变化趋势，而不仅仅是平均值的变化。这对于理解极端事件（如洪水或干旱）的影响尤其重要，因为这些事件往往集中在分布的两端。通过这种方式，可以更全面地评估降水和径流之间的关系，以及它们如何受到气候变化的影响。 文章可能会深入探讨如何构建分位数回归模型，包括选择合适的分位数水平、处理缺失值和异常值的方法，以及模型的验证和解释。此外，作者可能会讨论分位数回归在识别不同时间尺度上降水和径流变化模式中的应用，例如季节性或年际变化。 最后，基于分位数回归的分析结果可能有助于水资源管理和防洪决策，提供关于未来气候情景下径流变化的预测，从而帮助制定适应策略。这种方法不仅对潘家口水库流域，而且对其他受气候变化影响的地区，都具有重要的实践意义和理论价值。 本文通过引入分位数回归技术，为理解和分析降水和径流变化提供了新的工具，有望深化我们对气候变化影响的认识，促进水资源的可持续管理。