改进离散蜜蜂算法优化混合流水线工期

141 浏览量更新于2024-08-29 收藏 902KB PDF 举报

本文探讨了一种针对混合流水车间问题（Hybrid Flow Shop Problem, HFS）的优化方法，该问题在制造系统中具有广泛的应用，被公认为典型的NP-hard组合优化问题。混合流水车间是指工作流程中包含了多种类型的设备和工件转移路径，使得任务调度复杂化。研究者们提出了一个改进的离散人工蜂群算法（Improved Discrete Artificial Bee Colony, IDABC），该算法旨在通过有效地解决HFS问题来最小化生产周期（Makespan），即完成所有任务所需的时间。算法的核心思想是结合新颖的差分进化（Differential Evolution）与改良的变量邻域搜索（Modified Variable Neighborhood Search, MVNS），这两种技术的融合旨在增强搜索的全局性和局部探索能力。在IDABC中，工蜂（ Employed Bees）和侦察蜂（Scout Bees）分别负责寻找新的可能解和探索未知区域。工蜂通过差分进化生成新解，同时利用MVNS进行局部优化，以保持解的质量。侦察蜂则在遇到无法改进的解时，会进行破坏与重建（Destruction and Construction），这是一种创新的淘汰机制，有助于跳出局部最优，寻求全局最优解。为了评估算法的有效性，研究者还进行了正交试验设计，这有助于量化不同参数设置对算法性能的影响，确保了结果的可靠性和算法的稳健性。经过一系列的接收、修订和接受过程，最终于2014年6月25日在网上发表。这篇研究论文提出了一种创新的混合流水车间问题求解策略，通过结合差分进化和变量邻域搜索，提高了离散人工蜂群算法在解决实际生产环境中的复杂调度问题时的性能，为制造业提供了实用的工具，有望降低生产成本并提高生产效率。

ðiÞ;1

¼ min

k ¼ 1;2;…m

fIM

k;1

gþp

ðiÞ;1

¼ arg min

k ¼ 1;2;…m

fIM

k;1

¼ C

ðiÞ;1

i ¼ m

þ1; m

þ2; …n ð3Þ

ðiÞ¼gðC

j  1

ðiÞ;j  1

Þ i ¼ 1; 2; …n; j ¼ 2; 3; …s ð4Þ

ðiÞ;j

¼ C

ðiÞ;j  1

þp

ðiÞ;j

i;j

¼ C

ðiÞ;j

(

i ¼ 1; 2; …m

; j ¼ 2; 3; …s ð5Þ

ðiÞ;j

¼ max fC

ðiÞ;j  1

; min

k ¼ 1;2;…m

fIM

k;j

ggþp

ðiÞ;j

¼ arg min

k ¼ 1;2;…m

fIM

k;j

¼ C

ðiÞ;j

i ¼ m

þ1; m

þ2; …n; j ¼ 2; 3; …s

ð6Þ

where π

is the job permutation at the stage j; π

(i) is the ith job in

the job permutation π

; C

ðiÞ;j

is the completion time of job π

(i)at

the stage j; IM

i,j

represents the idle moment of machine i at the

stage j; NM

denotes the serial number of earliest available

machine at the moment at the stage j; the function S

(i)¼g(S

j 1

(i))

(i¼1,2,…, n) means that S

is the permutation of i (i¼1,2,…n) at the

stage j based on the ascending order of S

j 1

(i)(i¼1,2,…n) at the

stage j 1; and argmin

fIM

g stands for the argument of the

minimum, i.e. the set of points of the given argument for which

the given function attains its minimum value.

Eq. (1) deﬁnes the objective function which to minimize the

makespan C

max

. In above recursive equations (2)–(6), the authors

ﬁrstly calculate the completion time of jobs at the stage one, then

that of the stage two, until the last stage. To illustrate the model

and the issues described above, the authors consider a simple

example of the HFS problem with 4 jobs and 3 stages. The number

of machines at each stage is 2 and the processing time p

i,j

is given

i;j

241

542

215

223

Suppose the job sequence at the stage one π

¼(2, 1, 3, 4) is

given. Then the makespan C

max

is calculated as follows (the Gantt

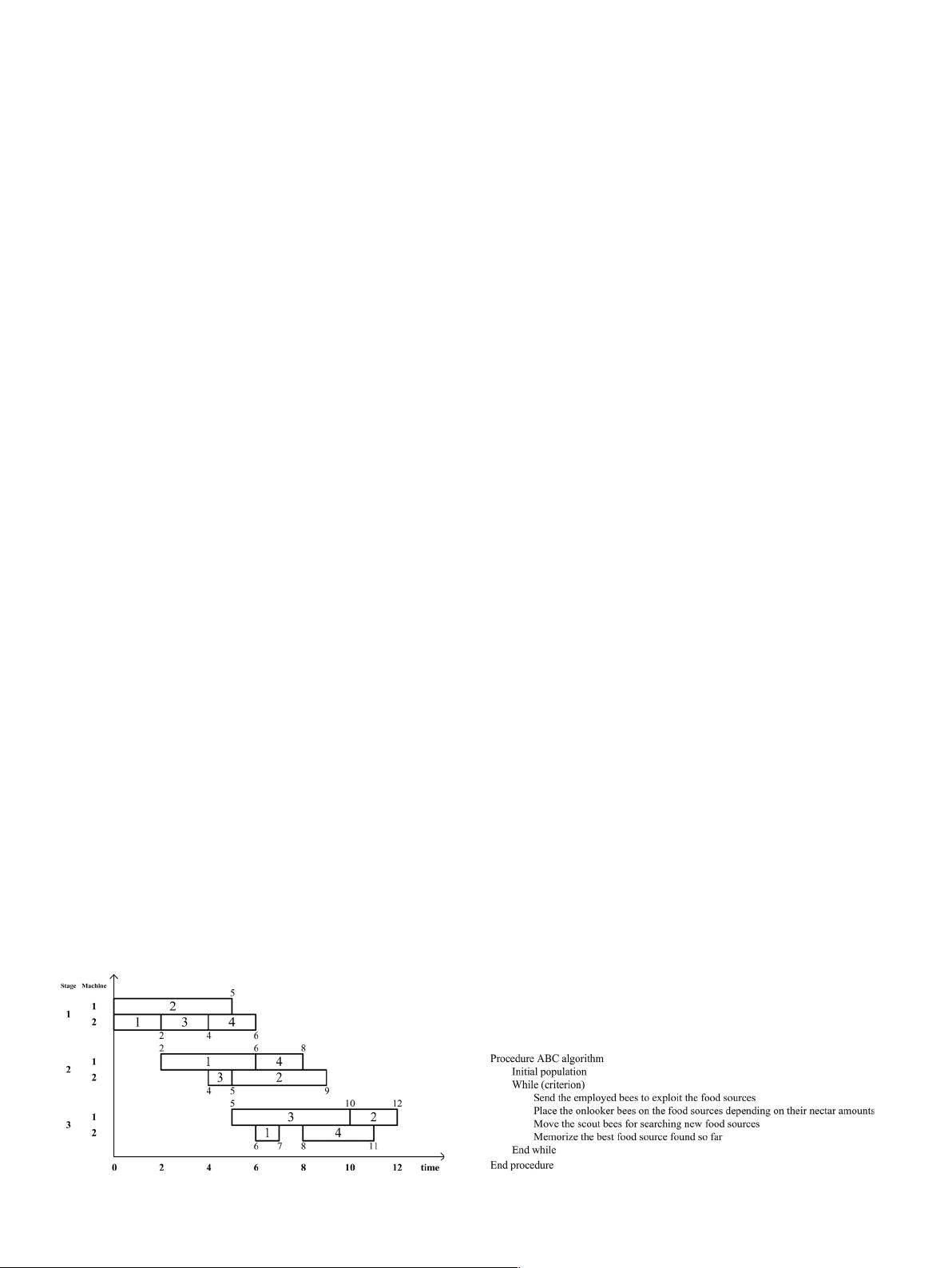
chart is shown in Fig. 1):

Stage 1

ð1Þ;1

¼ IM

1;1

¼ p

ð1Þ;1

¼ 5

ð2Þ;1

¼ IM

2;1

¼ p

ð2Þ;1

¼ 2

ð3Þ;1

¼ min fIM

1;1

; IM

2;1

gþp

ð3Þ;1

¼ 2 þ2 ¼ 4

¼ arg min fIM

1;1

; IM

2;1

g¼2

2;1

¼ C

ð3Þ;1

¼ 4

ð4Þ;1

¼ min fIM

1;1

; IM

2;1

gþp

ð4Þ;1

¼ 4 þ2 ¼ 6

¼ð1; 3; 2; 4Þ

Stage 2

ð1Þ;2

¼ IM

1;2

¼ C

ð1Þ;1

þp

ð1Þ;2

¼ 2þ4 ¼ 6

ð2Þ;2

¼ IM

2;2

¼ C

ð2Þ;1

þp

ð2Þ;2

¼ 4þ1 ¼ 5

ð3Þ;2

¼ max fC

ð3Þ;1

; min fIM

1;2

; IM

2;2

ggþp

ð3Þ;2

¼ 5þ4 ¼ 9

¼ arg min fIM

1;2

; IM

2;2

g¼2

2;2

¼ C

ð3Þ;2

¼ 9

ð4Þ;2

¼ max fC

ð4Þ;1

; min fIM

1;2

; IM

2;2

ggþp

ð4Þ;2

¼ 6þ2 ¼ 8

¼ð3; 1; 4; 2Þ

Stage3

ð1Þ;3

¼ IM

1;3

¼ C

ð1Þ;2

þp

ð1Þ;3

¼ 5þ5 ¼ 10

ð2Þ;3

¼ IM

2;3

¼ C

ð2Þ;2

þp

ð2Þ;3

¼ 6þ1 ¼ 7

ð3Þ;3

¼ max fC

ð3Þ;2

; min fIM

1;3

; IM

2;3

ggþp

ð3Þ;3

¼ 8þ3 ¼ 11

¼ arg min fIM

1;3

; IM

2;3

g¼2

2;3

¼ C

ð3Þ;3

¼ 11

ð4Þ;3

¼ max fC

ð4Þ;2

; min fIM

1;3

; IM

2;3

ggþp

ð4Þ;3

¼ 10þ2 ¼ 12

Thus the makespan is:

max

ðπ

Þ¼ max fC

ð1Þ;3

; C

ð2Þ;3

; C

ð3Þ;3

; C

ð4Þ;3

g¼C

ð4Þ;3

¼ 12

3. The improved discrete artiﬁcial bee colony (IDABC)

algorithm for the HFS problem

The ABC algorithm inspired by the foraging behaviors of real

honey bees is originally designed for the continuous nature of

optimization problems. In a real bee colony, there are some tasks

done by specialized individuals. Bees try to maximize the nectar

amount unloaded to the food stores in the hive by the division of

labor and self-organization, which are essential components of

swarm intelligence [41]. The colony of artiﬁcial bees in the ABC

algorithm contains three groups of bees, namely, the employed

bees, the onlooker bees, and the scout bees. Each of them plays

different roles in the process: the employed bees ﬂy onto the

sources which they are exploiting; the onlooker bees waiting in

the hive are responsible for deciding whether a food source is

promising by watching the dances performed by the employed

bees; and the scout bees choose sources randomly by means of

some internal motivations or possible external clues. Both the

onlooker bees and the scout bees are also called unemployed bees.

A food source in the search place corresponds to a solution of the

optimization problem, and the nectar amount of the food source

corresponds to the ﬁtness of the solution. The processes of the ABC

algorithm can be shown in pseudo-code as Fig. 2.

Following the above procedure for the continuous function

optimization, in this article the authors propose an improved

discrete version of the ABC algorithm for the HFS problem. It is

shown in details below.

3.1. Individual representation and initialization

Owing to its continuous nature of the basic ABC algorithm,

researchers always converted the real domain into the discrete

domain when it is applied to the discrete optimization. And this

overhead makes the algorithms complicated. The model of the HFS

problem is formulated by using the vector representation in the

previous section. As a result, the authors adopt this representation

Fig. 1. An example of HFS problem with 4 jobs and 3 stages. Fig. 2. The procedure of basic ABC algorithm.

Z. Cui, X. Gu / Neurocomputing 148 (2015) 248–259250

剩余11页未读，继续阅读

weixin_38625164

粉丝: 4
资源: 910

改进离散蜜蜂算法优化混合流水线工期

离散人工蜂群算法求解资源时变的项目调度问题

一种改进的离散人工蜂群算法，可在有限缓冲区的置换流水车间调度中最大程度地减少总流时间

一种改进的人工蜂群算法，可最大程度地减少时间成本

一种改进的人工蜂群算法，求解带动态操作跳过的混合柔性流水车间

离散人工蜂群算法，用于最小化阻塞流水车间调度中的总流时间

求解makepan最小的混合Flowshop调度问题的一种新的离散人工蜂群算法

ArtificialBeeColonyAlgorithm：对人工蜂群算法的理解和改进人工蜂群算法的思想，以及C Java Python-对人工蜂群算法的理解和改进人工蜂群算法的思路以及人工蜂群算法及其改进算法的CJavaPython实现人工蜂群算法的实现及其改进算法

人工蜂群算法（改进版）.zip_人工蜂群优化_人工蜂群算法_改进蜂群_改进蜂群算法_蜂群算法

具有维护活动的多目标柔性作业车间调度问题的离散人工蜂群算法

人工蜂群算法改进版.rar_人工蜂群_人工蜂群改进_改进人工蜂群_蜂群_蜂群算法

最新资源