MATLAB中可行方向法求解优化问题详解
版权申诉
14 浏览量
更新于2024-06-26
收藏 506KB DOCX 举报
本篇文档主要介绍了如何使用MATLAB实现基于可行方向法的极值问题求解。在实际的工程优化设计中,当设计变量和约束条件数量增加时,传统的随机方向搜索法和复合形法可能不再高效。可行方向法因其在可行域内快速收敛和优良的性能,成为了解决这类复杂约束非线性优化问题的有效手段,特别适用于大型优化问题。
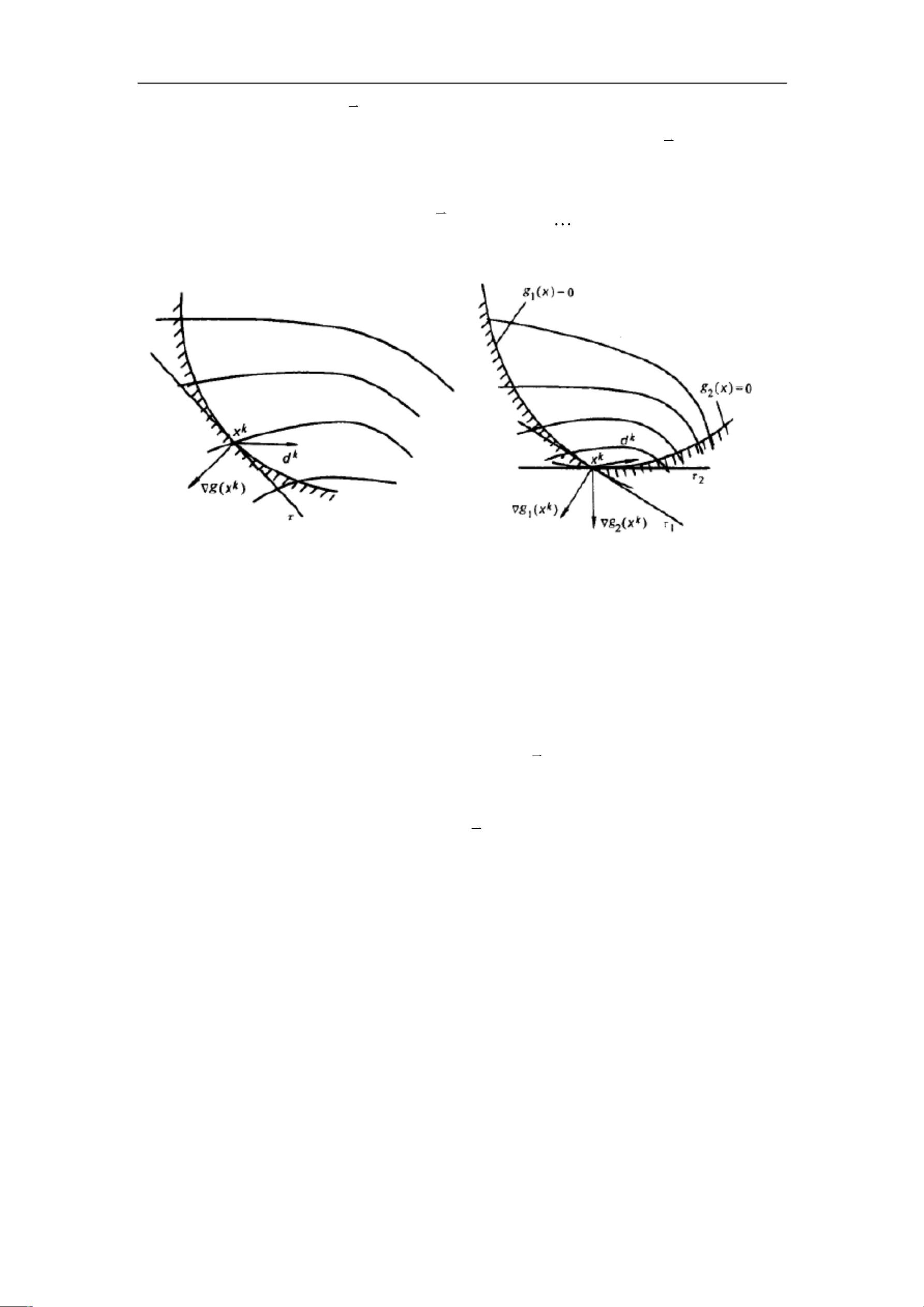
文章首先阐述了可行方向法的基本数学思想,它从初始点X开始,通过沿负梯度方向移动,并根据约束函数和目标函数特性采取不同的搜索策略。策略一是如果新点保持在可行域内,则继续沿该方向优化;如果新点超出可行域,则调整到最近的约束面上并重复,直到梯度小于预设阈值。另一种策略是当新点在可行域外时,以最大步长到达另一个约束面,继续搜索,直到满足特定的K-T条件。
1.2节中详细讨论了产生可行方向和步长的数学原理。关键在于定义一个方向d(k)对于点X的可行性,即存在某个正数A使得方向d(k)对所有0≤A≤A都满足约束条件。具体来说,当方向d(k)与起作用的约束梯度不平行时,通过线性规划和约束最优步长法在MATLAB中实现这一过程。
文档还涉及到了对具有线性约束的非线性规划问题的处理,给出了一个简单的计算公式,表明了如何通过调整系数来确保新点始终在可行域内或向目标方向移动。
本文旨在提供一个实践性的教学指南,通过MATLAB编程技术,帮助读者理解并应用可行方向法解决优化设计中的实际问题,提升求解效率。关键词包括:可行方向法、MATLAB、优化方法,强调了这种方法在工程优化中的重要性和实用性。
201 浏览量
604 浏览量
点击了解资源详情
2023-03-10 上传
2023-03-10 上传
258 浏览量
不吃鸳鸯锅
- 粉丝: 8562
- 资源: 2万+
最新资源
- On11-TodasEmTech-s7-API-GET:API简介
- mai-cc60,matlab混沌加密源码,matlab源码之家
- Linux系统软键盘源码分享
- crds:用于HST和JWST的校准参考数据系统
- nsvue-colors:App feito com {N} que simplifica作为十六进制核心
- 基于Java实现的离散数学测试实验.zip
- AS_EF:EF分配材料
- TM1812_led.zip
- forever-webui, 一个简单的用于高效NodeJS流程管理的web UI.zip
- matlab代码sqrt-ecc_vs_rsa:公钥密码学的比较分析
- any:匿名对象生成器。 Tdd Toolkit的Any类的继承者
- sql-query-test-application
- OlaMundo:PrimeiroRepositorioVerionado
- TRANSMIT-BEAMFORMING,分布参数系统matlab源码,matlab源码怎么用
- 任务列表:使用Vue Native添加和删除任务列表
- RocketPay:NLW排名第4的天然药水