174 Part A Basic Principles and Materials
experiments not only demonstrated the significance of
THG for efficient, guided-wave frequency tripling of
femtosecond laser pulses, but also revealed several
new interesting nonlinear-optical phenomena. The third-
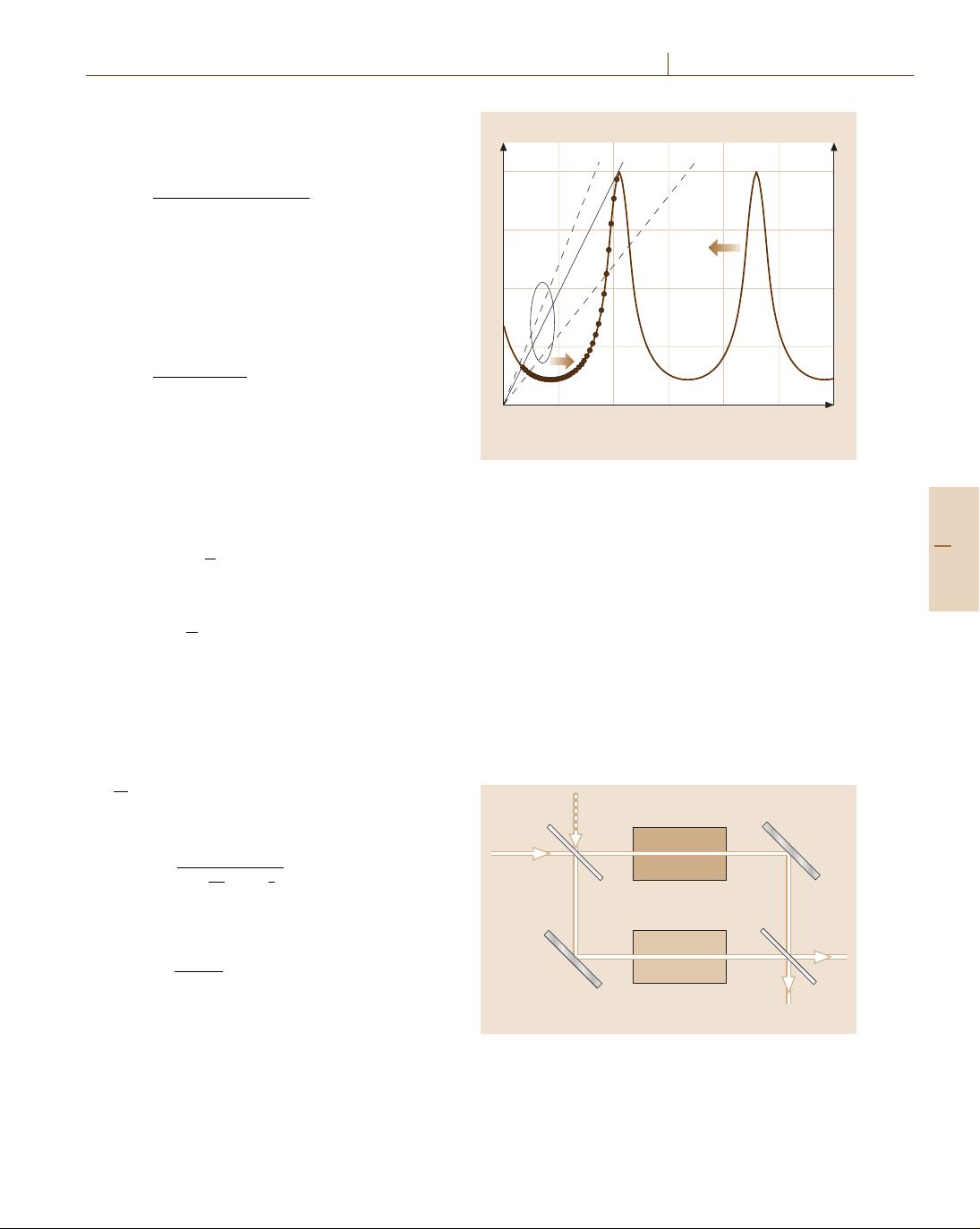
harmonic signal has been shown to display asymmetric
spectral broadening [4.51, 52] or even a substantial
frequency shift. We will demonstrate here that such
a behavior is a universal intrinsic feature of multi-
mode guided-wave THG. Based on the arguments of
the slowly varying envelope approximation (SVEA),
we will show that the sign and the absolute value of
the third-harmonic frequency shift, observed in many
PCF experiments, is controlled by the phase- and group-
index mismatch for the interacting pair of pump and
third-harmonic modes. The possibility to tune the fre-
quency of the main spectral peak in the spectrum of the
third harmonic by varying the group-velocity mismatch
is a unique property of THG-type processes, which is not
typical of standard parametric FWM processes, where
the first-order dispersion terms cancel out of the bal-
ance of the field momenta. New regimes of THG will
be identified with no signal produced at the central fre-
quency of the third harmonic 3ω
0
and with the pump
energy efficiently converted to spectrally isolated nar-
rowband frequency components, which can be tuned
within a spectral range of several tens of terahertz from
the 3ω
0
frequency.
We start with qualitative argumentsillustratingphase
matching for third-harmonic generation generalized to
include the phase and group-velocity mismatch of the
pump and third-harmonic fields, as well as the Kerr ef-
fect, broadening the pump spectrum through SPM.We
represent the wave numbers (or the propagation con-
stants of guided modes in a waveguide regime) k
p
and
k
h
at the frequencies of the pump field and the third
harmonic as
k
p
(
ω
)
≈k
(
ω
0
)
+v
−1
p
Ω/3 +κ
SPM
P , (4.117)
k
h
(
3ω
)
≈k
(
3ω
0
)
+v
−1
h
Ω +2κ
XPM
P , (4.118)
where ω
0
is the central frequency of the pump
field; v
p,h
= (∂k/∂ω)
−1
ω
0
,3ω
0
are the group velocities
of the pump and its third harmonic; Ω =3ω −3ω
0
;
κ
SPM
= ω
0
n
2
/cS
eff
and κ
XPM
= 3ω
0
¯
n
2
/cS
eff
are the
SPM and XPM nonlinear coefficients (S
eff
is the ef-
fective beam, or mode, area and n
2
and
¯
n
2
are the
nonlinear refractive indices at ω
0
and 3ω
0
, respectively);
and P is the power of the pump field. In writing (4.117)
and (4.118), we neglect group-velocity dispersion and
higher-order dispersion effects, as well as the SPM of the
third-harmonic field. With n
2
≈
¯
n
2
, the phase mismatch
is then given by
∆k =k
h
−3k
p
≈∆k
0
+ξΩ +3κ
SPM
P , (4.119)
where ∆k
0
=k(3ω
0
) −3k(ω
0
) is the phase mismatch
of the pump and third-harmonic wave numbers at the
central frequencies of these fields and ξ =v
−1
h
−v
−1
p
is
the group-velocity mismatch.
As can be seen from (4.119), the group delay of the
pump and third-harmonic pulses is an important fac-
tor in THG momentum conservation. In this respect, the
balance of momenta for THG radically differs from stan-
dard phase-matching conditions for parametric FWM
processes [4.23], where the first-order dispersion order
terms cancel out, reducing the FWM momentum balance
to group-velocity dispersion (GVD)-related issues.
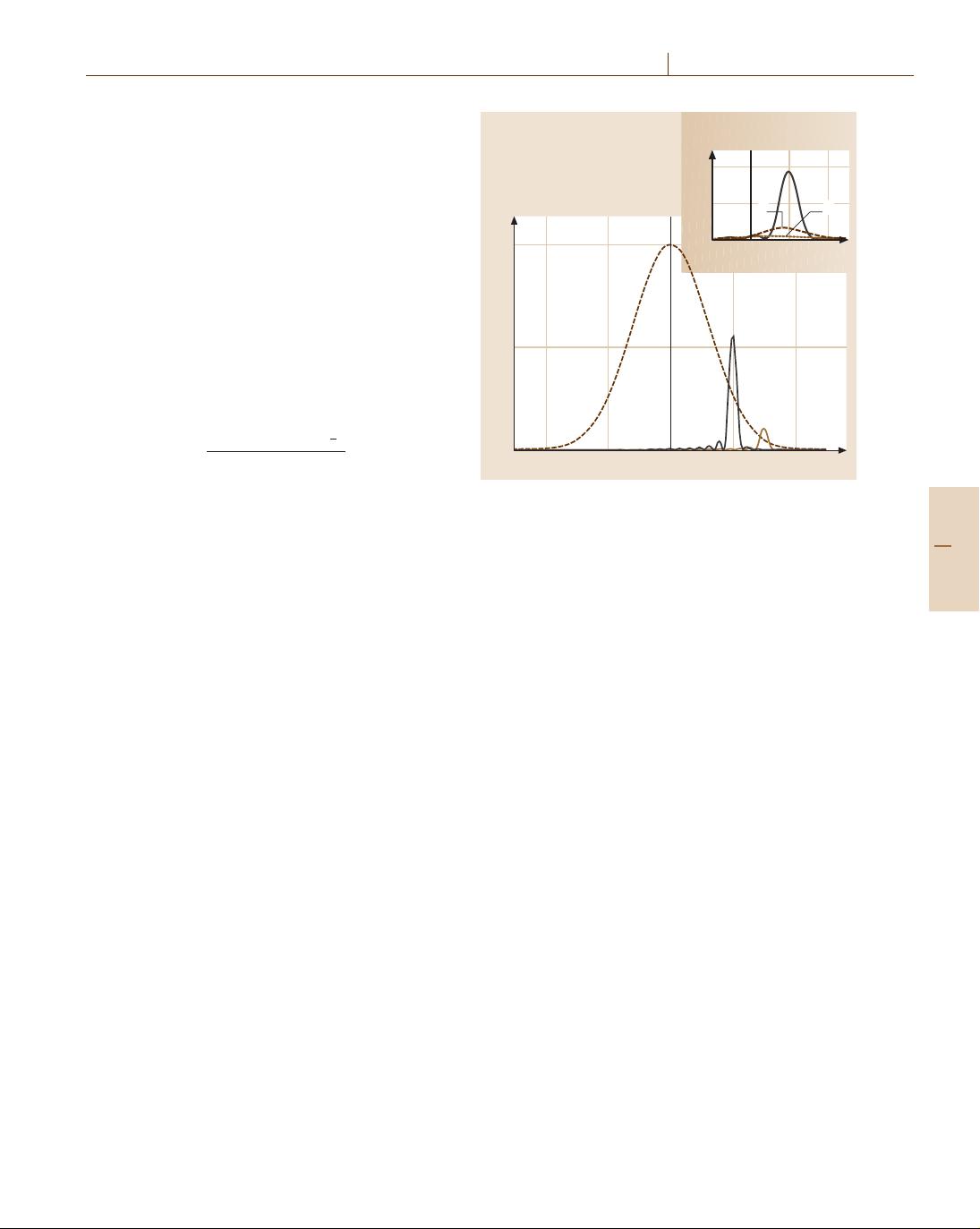
The phase-matching condition (4.119) suggests the
possibility of substantially frequency shifting the max-
imum in the spectrum of the third harmonic. However,
the amplitude of an Ω-shifted spectral component in
the spectrum of the third harmonic and, hence, the ef-
ficiency of Ω-shifted peak generation is determined by
the spectrum of the pump field. To specify this depen-
dence, we proceed with an SVEA analysis of THG in the
field of SPM-broadened pump field by writing SVEA
coupled equations for the envelopes of the pump and
third-harmonic fields, A(t, z)andB(t, z):
∂
∂t
+
1
ν
p
∂
∂z
A =iγ
1
A
|
A
|
2
, (4.120)
∂
∂t
+
1
ν
h
∂
∂z
B =iβ
(
A
)
3
exp
(
−i∆k
0
z
)
+2iγ
2
B
|
A
|
2
, (4.121)
where v
p
and v
h
are the group velocities of the pump and
third-harmonic pulses, respectively, and γ
1
, γ
2
and β are
the nonlinear coefficients responsible for SPM, XPM,
and THG, respectively; and ∆k =k
h
−3k
p
is the phase
mismatch (or the difference of propagation constants in
the guided-wave regime) in the absence of the nonlinear
phase shifts of the pump and third-harmonic fields.
Solution of (4.120)and(4.121) yields [4.24, 55]
A
t
p
, z
= A
0
t
p
exp
iϕ
SPM
t
p
, z
, (4.122)
B
(
t
h
, z
)
=iσ
z
0
dz
A
3
0
t
h
+ξz
×exp
−i∆β
0
z
+3iϕ
SPM
t
h
+ξz
, z
+iϕ
XPM
t
h
, z
, z
)
,
(4.123)
where t
l
=(t −z/v
l
) with l = p, h for the pump and the
field, respectively; A
0
(t) is the initial-condition envelope
Part A 4.4