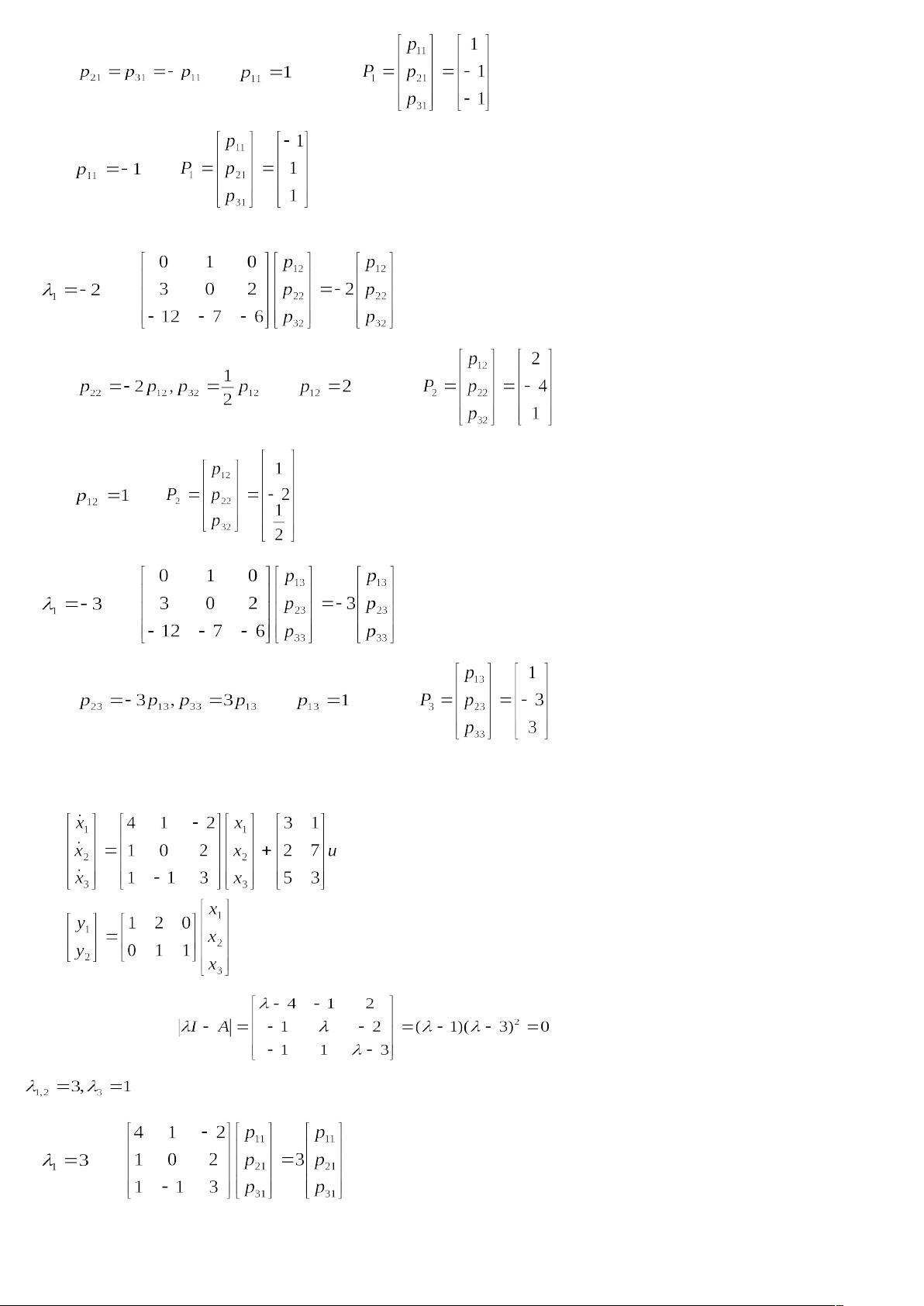现代控制理论习题解答与状态空间建模

"现代控制理论第三版答案" 本资料提供了《现代控制理论》第三版教材的相关习题解答，涵盖了状态空间表达式、模拟结构图、传递函数、约旦标准型等多个核心概念。以下是对这些知识点的详细解释： 1. **状态空间表达式**：状态空间表达式是控制系统理论中描述系统动态行为的一种方法。它通过一组线性常微分方程（或差分方程）来表示系统的状态随时间的变化，通常形式为\[ \dot{x}(t) = Ax(t) + Bu(t) \]，其中，\( x(t) \)是状态向量，\( A \)是状态矩阵，\( B \)是输入矩阵，\( u(t) \)是输入向量。例如，问题1-1、1-2和1-4中都涉及到了如何根据系统结构构建状态空间表达式。 2. **模拟结构图**：模拟结构图是用图形方式表示线性系统的数学模型，它由电阻、电容、电感、运算放大器等基本元件组成，用来直观展示信号的流动和处理过程。在问题1-1、1-5和1-6中，都给出了如何将问题转化为模拟结构图的步骤。 3. **传递函数**：传递函数是线性定常系统动态特性的频率域表示，它描述了系统输出对输入的拉普拉斯变换比。在问题1-5和1-6中，除了状态空间表达式，还求出了传递函数，这对于分析系统响应和设计控制器非常重要。 4. **约旦标准型**：约旦标准型是矩阵的一种特殊形式，对于线性系统的状态空间表达式，它可以提供关于系统动态特性的更深入理解，包括稳定性、特征值和特征向量等信息。问题1-9展示了如何将状态矩阵化为约旦标准型，并且在问题1-6中，还要求实现系统的约旦标准型模拟结构。 5. **特征矢量和特征值**：特征值和特征向量是描述线性变换性质的重要工具。特征值是线性变换下保持向量长度不变的比例因子，特征向量则是对应这个比例因子的向量。在问题1-8中，计算了矩阵的特征矢量，这在确定系统的动态特性、稳定性分析和控制设计中非常关键。 6. **状态方程与输出方程**：状态方程描述系统内部状态变量随时间的变化，而输出方程则关联输入和输出的关系。例如，在问题1-2中，以电感电流和电容电压为状态变量，以电阻电压为输出，建立了状态方程和输出方程。 这些习题解答涵盖了现代控制理论的基础知识，对于学习者理解和应用控制理论概念具有指导意义。通过解决这些问题，可以深化对系统建模、分析和设计的理解，为实际工程问题的解决打下坚实基础。