JavaScript数据结构和算法之二叉树详解

二叉树详解 二叉树是一种常用的数据结构，它是一种树形结构，具有各自的特点和应用场景。下面是对二叉树的详细介绍： **二叉树的概念** 二叉树（Binary Tree）是n（n>=0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。 **二叉树的特点** 每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点。二叉树中每一个节点都是一个对象，每一个数据节点都有三个指针，分别是指向父母、左孩子和右孩子的指针。每一个节点都是通过指针相互连接的。相连指针的关系都是父子关系。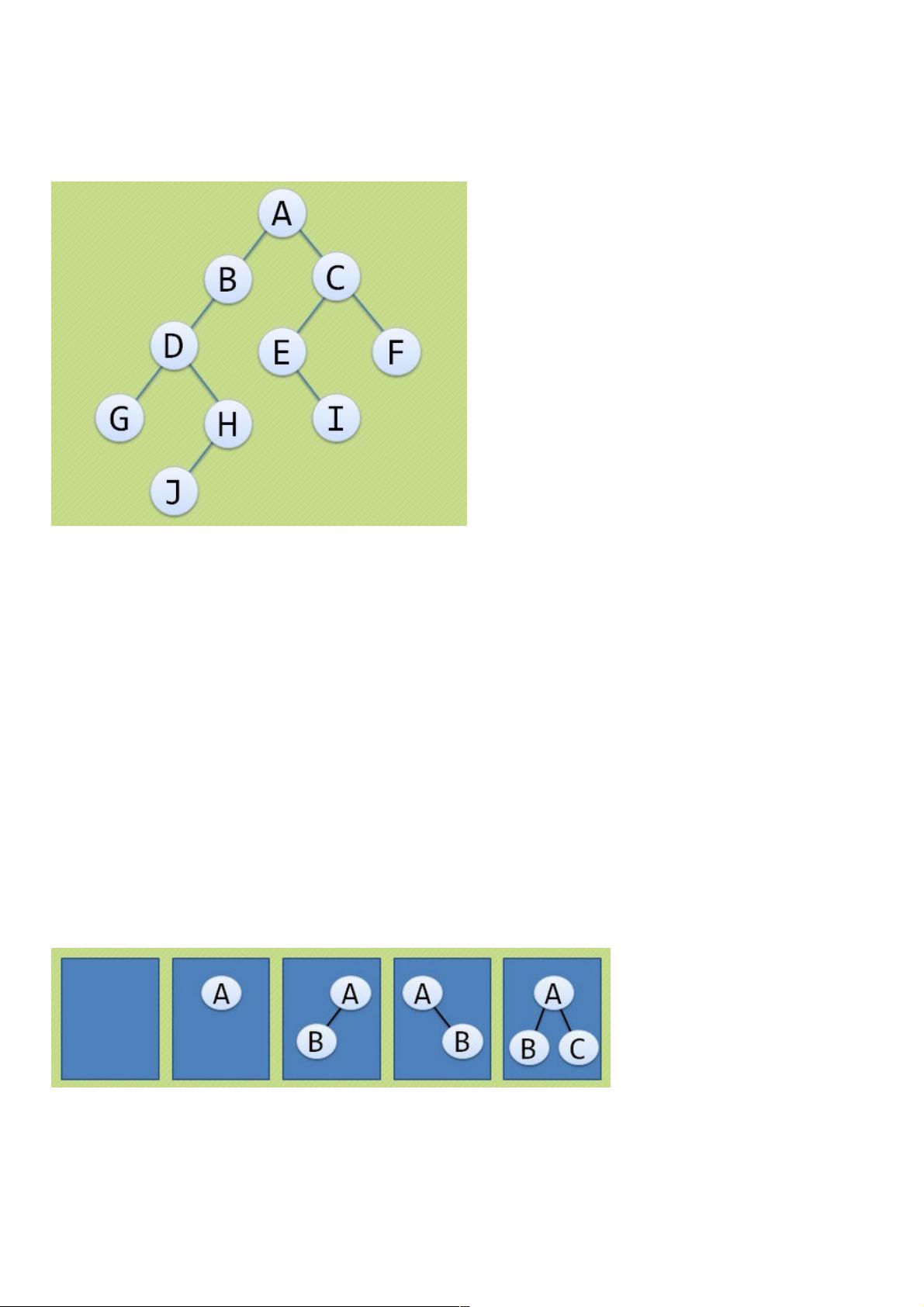 **二叉树节点的定义** 二叉树节点定义如下： ```c struct BinaryTreeNode { int m_nValue; BinaryTreeNode* m_pLeft; BinaryTreeNode* m_pRight; }; ``` **二叉树的五种基本形态** 1. 空二叉树 2. 只有一个根结点 3. 根结点只有左子树 4. 根结点只有右子树 5. 根结点既有左子树又有右子树 **特殊二叉树** 1. 斜树：如上面倒数第一副图的第2、3小图所示。 2. 满二叉树：在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。 3. 完全二叉树：完全二叉树是指最后一层左边是满的，右边可能满也可能不满，然后其余层都是满的。一个深度为k，节点个数为2^k–1的二叉树为满二叉树（完全二叉树）。 **完全二叉树的特点** 1. 叶子结点只能出现在最下两层。 2. 最下层的叶子一定集中在左部连续位置。 3. 倒数第二层，若有叶子结点，一定都在右部连续位置。 4. 如果结点度为1，则该结点只有左孩子。 5. 同样结点树的二叉树，完全二叉树的深度最小。 **算法** 判断一棵二叉树是否为完全二叉树的算法： ```c bool is_complete(tree* root) { queue q; tree* ptr; // 进行广度优先遍历（层次遍历），并把NULL节点也放入队列 q.push(root); while((ptr = q.pop()) != NULL) { q.push(ptr->left); q.push(ptr->right); } // 判断是否还有未被访问到的节点 while(!q.is_empty()) { // ... } } ``` **二叉树遍历** 二叉树遍历是指从根结点开始，按照某种顺序访问每个结点的过程。常见的二叉树遍历方法有先序遍历、中序遍历、后序遍历等。 **先序遍历** 先序遍历是指先访问根结点，然后访问左子树和右子树。 **中序遍历** 中序遍历是指先访问左子树，然后访问根结点，最后访问右子树。 **后序遍历** 后序遍历是指先访问左子树和右子树，然后访问根结点。 二叉树是一种常用的数据结构，它有广泛的应用场景，例如文件系统、数据库、浏览器历史记录等。了解二叉树的概念、特点和遍历方法对编程和算法设计非常重要。