算法的时间与空间复杂度分析

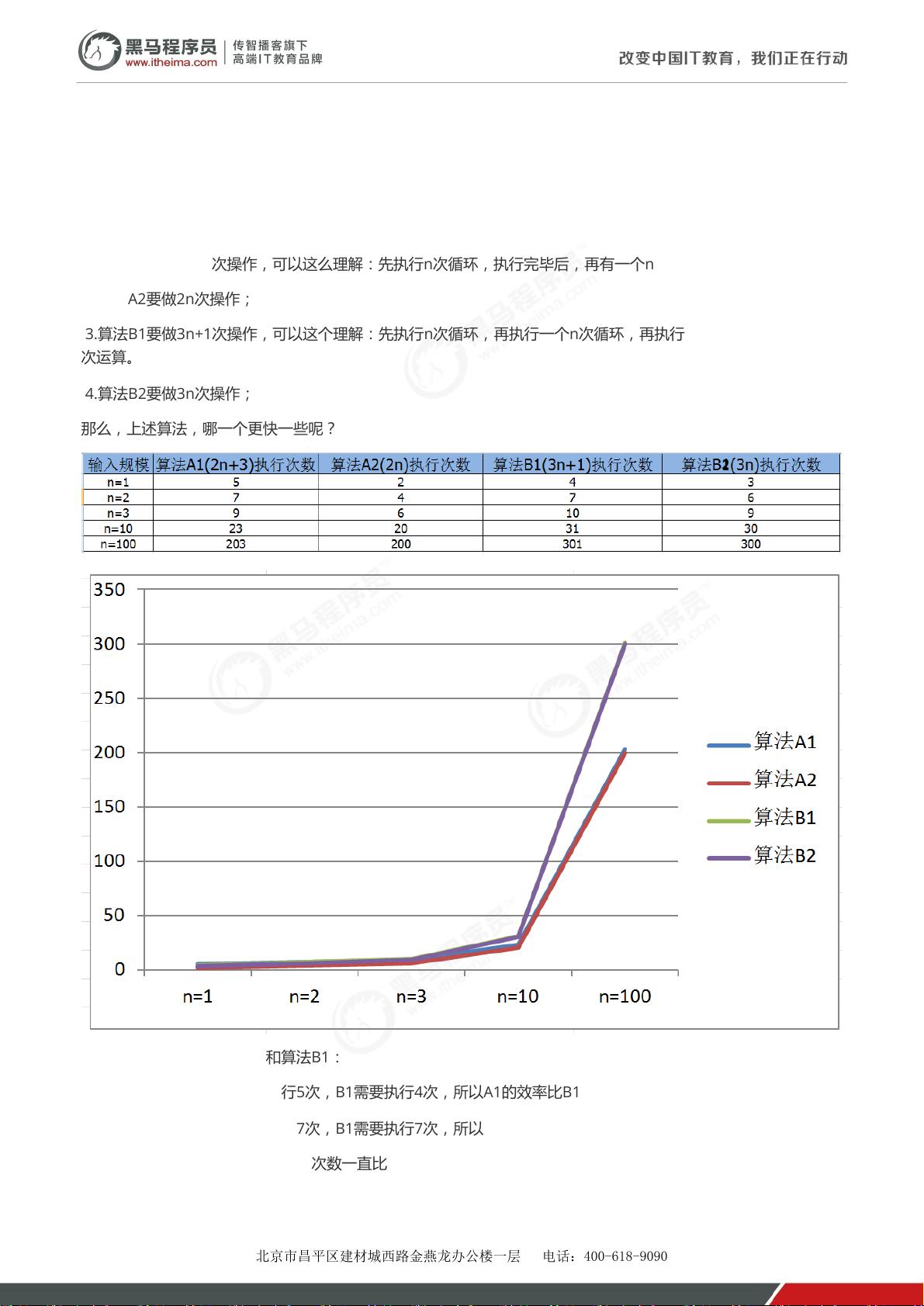
于算法本身的特性，即算法采用的策略和方案。在算法分析中，我们关注的主要就是算法的时间复杂度，它描述了算法执行时间与问题输入规模之间的关系。时间复杂度的分析通常忽略低阶项和常数项，只保留最高阶项，以简化分析过程。 对于给定的代码段，其主要部分是一个简单的for循环，用于计算1到n的累加和。这段代码的时间复杂度是O(n)，因为它包含了n次加法操作。这里的n是问题的输入规模，即循环变量的上限。当n增大时，执行时间会线性增加。这种直接与问题规模成正比的时间消耗被称为线性时间复杂度。 在实际应用中，我们希望找到更高效的算法，例如，如果要计算前n个自然数的平方和，使用一个嵌套循环的直观方法会导致时间复杂度为O(n^2)，而使用数学公式可以直接得到结果，时间复杂度为O(1)。这表明，即使在相同的硬件环境下，不同的算法设计可以带来显著的性能差异。 时间复杂度分析不仅仅用于比较不同算法的效率，也是评估算法能否在实际场景中应用的重要标准。例如，如果问题的输入规模非常大，那么一个时间复杂度为O(n^2)的算法可能就无法在可接受的时间内完成任务，而一个时间复杂度为O(log n)的算法则可能更合适。 除了时间复杂度，我们还需要关注算法的空间复杂度，这是算法在执行过程中额外需要的存储空间与问题输入规模的关系。空间复杂度的分析同样忽略低阶项和常数项。例如，上述代码的空间复杂度为O(1)，因为它只使用了几个固定的变量，不随n的增大而增加。 在进行算法分析时，我们通常采用大O记法来表示时间复杂度和空间复杂度，如O(1)、O(n)、O(log n)、O(n log n)、O(n^2)等。大O记法提供了一个相对的度量标准，而不是绝对的执行时间或空间大小，因此它能够跨平台、跨硬件环境地比较算法效率。 算法分析是理解和优化程序性能的关键步骤，它帮助我们理解算法在不同输入规模下的行为，并为我们选择和设计更有效的算法提供了理论基础。在实际开发中，结合时间复杂度和空间复杂度的考量，我们可以做出更加明智的决策，以实现程序的高效运行。