"构建队列：数据结构中栈和队列详解与完整算法"

建队的完整算法主要涉及数据结构中的栈和队列。栈和队列是两种常用的数据结构，用于存储和管理数据元素。在建队的完整算法中，我们需要了解如何初始化队列，进行入队和出队操作以及如何判断队列是否为空或已满。 首先，我们来介绍一下栈和队列的基本概念。栈是一种后进先出（LIFO）的数据结构，即最后入栈的元素最先出栈。栈的插入和删除操作只能在栈顶进行。而队列是一种先进先出（FIFO）的数据结构，即最先入队的元素最先出队。队列的插入操作在队尾进行，而删除操作在队头进行。 在建队的完整算法中，我们首先需要初始化队列。初始化队列需要定义一个队列结构，并分配内存空间。这可以通过以下函数实现： ``` Status InitQueue ( SqQueue &Q ) { Q.base = (QElemType *)malloc(MAXQSIZE * sizeof(QElemType)); if (!Q.base) exit(OVERFLOW); Q.front = Q.rear = 0; return OK; } ``` 在以上代码中，SqQueue表示队列结构，QElemType为队列元素的类型，MAXQSIZE为队列的最大长度。该函数首先分配队列的存储空间，并将队头和队尾指针初始化为0。如果分配空间失败，则程序退出。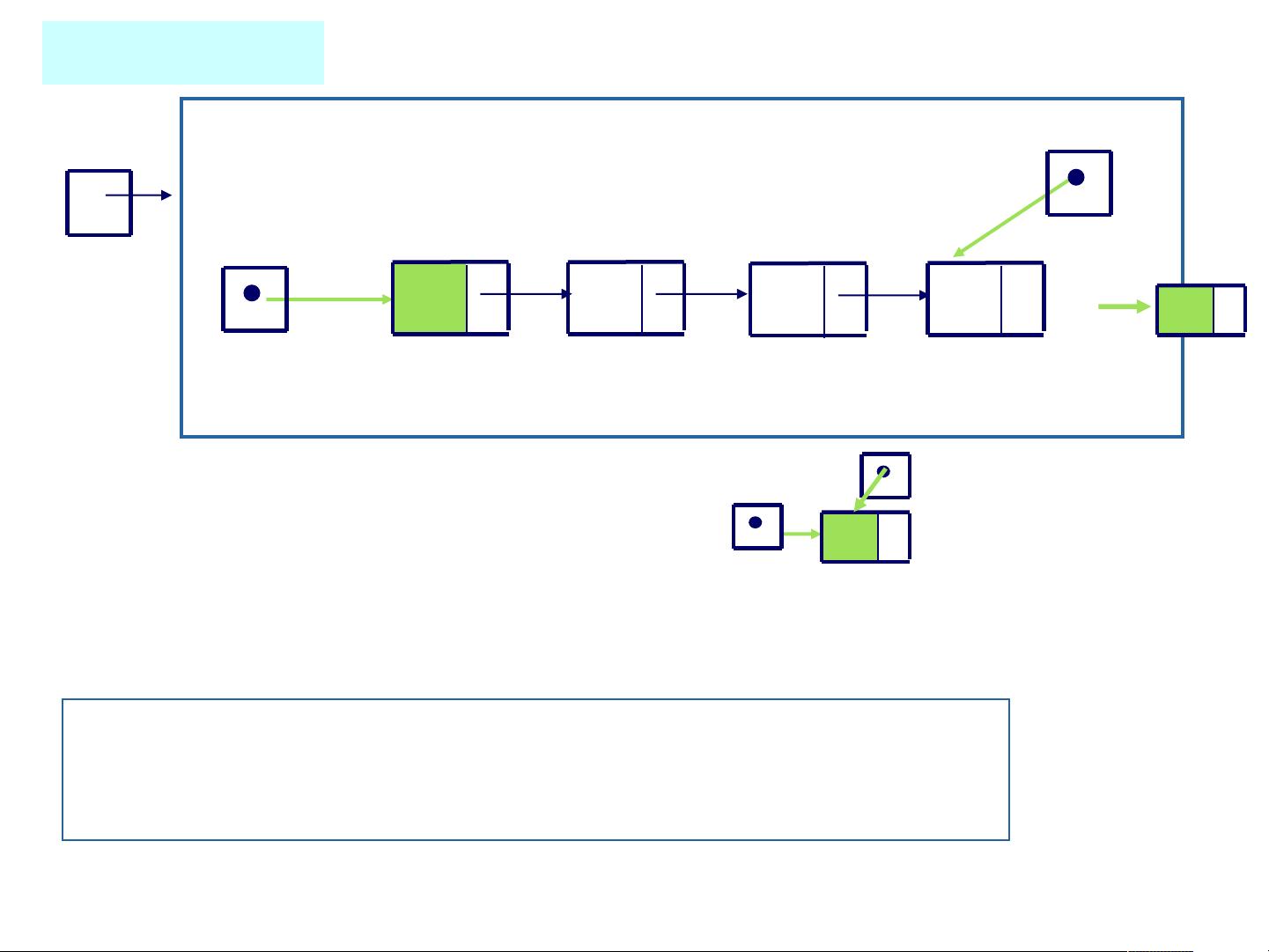 接下来是入队和出队操作。入队操作将元素加入队列的队尾，出队操作将元素从队列的队头删除。这两个操作可以通过以下函数实现： ``` Status EnQueue(SqQueue &Q, QElemType e) { if ((Q.rear + 1) % MAXQSIZE == Q.front) return ERROR; Q.base[Q.rear] = e; Q.rear = (Q.rear + 1) % MAXQSIZE; return OK; } Status DeQueue(SqQueue &Q, QElemType &e) { if (Q.front == Q.rear) return ERROR; e = Q.base[Q.front]; Q.front = (Q.front + 1) % MAXQSIZE; return OK; } ``` 在以上代码中，EnQueue函数实现入队操作，首先判断队列是否已满，如果队尾指针加1后等于队头指针，则表示队列已满。然后将元素e加入队尾，并将队尾指针后移一位。DeQueue函数实现出队操作，首先判断队列是否为空，如果队头指针等于队尾指针，则表示队列为空。然后将队头元素赋值给e，并将队头指针后移一位。 最后，我们需要判断队列是否为空或已满。这可以通过以下函数实现： ``` Status QueueEmpty(SqQueue Q) { if (Q.front == Q.rear) return TRUE; else return FALSE; } Status QueueFull(SqQueue Q) { if ((Q.rear + 1) % MAXQSIZE == Q.front) return TRUE; else return FALSE; } ``` 在以上代码中，QueueEmpty函数判断队列是否为空，如果队头指针等于队尾指针，则表示队列为空。QueueFull函数判断队列是否已满，如果队尾指针加1后等于队头指针，则表示队列已满。 综上所述，建队的完整算法涉及数据结构中栈和队列的操作，包括初始化队列、入队、出队以及判断队列是否为空或已满。通过了解这些基本操作，我们可以更好地理解和应用队列数据结构，提高算法的设计和实现能力。