数值计算课程设计：多项式插值的震荡现象分析

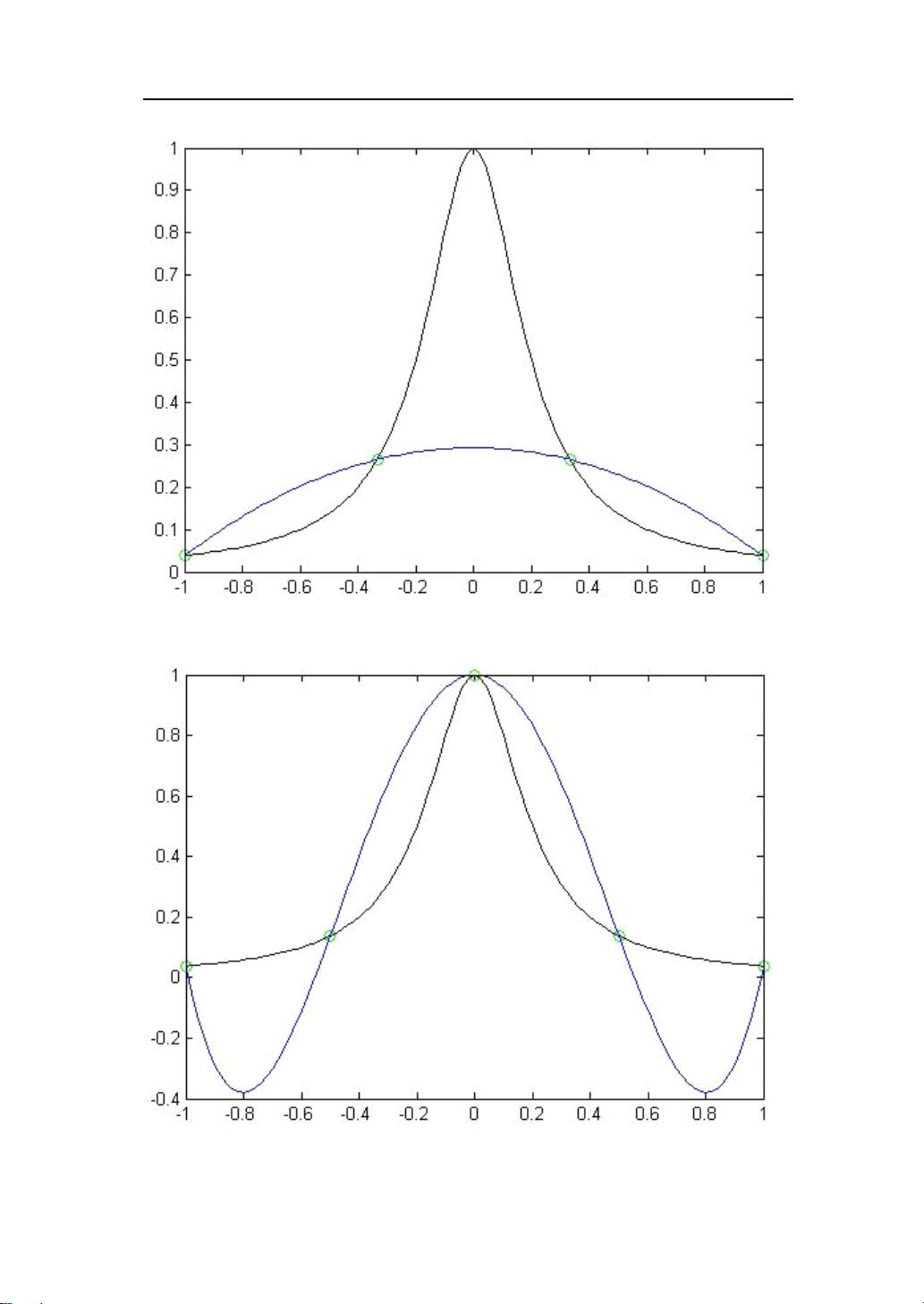
"这篇文档是关于数值计算课程设计的一个项目，专注于多项差值震荡现象的探讨。通过插值拟合的方法，分析了在不同节点数量下，拉格朗日插值多项式对函数逼近的效果，展示了插值过程中的振荡问题。" 在数值计算领域，多项差值是一种常见的技术，用于近似未知函数或数据点集。在这个课程设计中，学生通过研究多项差值的震荡现象来理解其内在机制。"震荡"是指在增加插值多项式的次数时，尽管理论上多项式应该更接近目标函数，但在某些情况下，插值误差可能会出现不降反增的现象，这被称为Runge现象。 Runge现象由德国数学家Carl Runge提出，他给出了一个简单的例子来阐述这个问题。在区间[-1,1]上，考虑函数f(x) = 1/(1 + x^2)，当使用拉格朗日插值法在等距节点上构建插值多项式时，随着节点数量的增加，插值多项式可能不再有效地逼近原函数，反而会在某些点上产生较大的误差。 拉格朗日插值是插值方法的一种，它基于一组给定的节点值来构造一个多项式，使得这个多项式在每个节点上都与原函数值相等。对于n个节点，拉格朗日插值多项式可表示为各个Lagrange基函数的线性组合。基函数ai(x)由节点定义，并确保在第i个节点上取值为1，而在其他节点上取值为0。 在实验部分，设计者们在[-1,1]区间上采用了等距节点，分析了不同分点数（n=2到8）时的最大误差L。结果显示，随着n的增加，误差L并不总是减小。例如，当n=2时，最大误差为0.646227；而当n=3时，误差增加到0.707014；然后在n=4时，误差下降到0.438353，之后在n=6时又上升到0.616920，最后在n=8时，误差激增到1.045174。这种误差的波动表明了Runge现象的存在，即在某些点上，高次插值多项式并不能提供更好的函数逼近。 通过这样的课程设计，学生们可以直观地了解数值计算中的一个核心挑战：如何在保证插值精度的同时避免振荡问题。解决这个问题的方法包括使用非均匀节点（如Chebyshev节点）、多项式外推或其他插值方法，如样条插值。这些方法可以有效地减少Runge现象的影响，提高插值多项式的稳定性和逼近质量。在实际应用中，理解和处理这种振荡现象对于优化数值算法、提高计算效率以及确保数值稳定性至关重要。