COL 10(1), 011002(2012) CHINESE OPTICS LETTERS January 10, 2012
Quadric surface projection model for fish-eye cameras
Tiantian Meng (孟孟孟甜甜甜甜甜甜)
1∗
, Jintao Jiang (蒋蒋蒋金金金涛涛涛)
2
, and Ming Yang (杨杨杨 鸣鸣鸣)
3
1
Faculty of Information Science and Engineering, Ningbo University, Ningbo 315211, China
2
Zhejiang High-tech Medical Optoelectronic Equipment Research and Development Center,
Ningb o University, Ningbo 315211, China
∗
Corresp onding author: tpmengtt@126.com
Received April 19, 2011; accepted June 10, 2011; posted online August 30, 2011
The curved surface projection model in fisheye image correction algorithm is presented. To analyze the
causes of distortion in existing models, we establish an ideal surface projection model and compare its
surface with the surfaces of existing models. Subsequently, feature points are obtained on the ideal surface
according to the relationship of coordinates of fish-eye image points and their ideal three-dimentional (3D)
p oints. Finally, the least square method is used to obtain a quadric surface and presents a quadric surface
projection model. The experiment shows that the corrected image of the new model is more similar to the
actual scene than the corrected images of previous models.
OCIS codes: 100.3008, 100.3010, 140.1135, 140.1488.
doi: 10.3788/COL201210.011002.
Fish-eye lenses have extremely short focal length and a
very wide field of view (FOV), which is generally close
to 180
◦
or even wider
[1]
. One single fish-eye image can
represent a large part of the surroundings. Thus, use
of fish-eye lens in detection and survey systems has at-
tracted considerable attention. Wu et al.
[2,3]
have used
fish-eye lens in automatic surveillance.
In order to obtain a large FOV, a fish-eye lens uses the
“non-similar” imaging thought. As a result, consider-
able barrel distortion in fish-eye images occurs. In recent
years, fish-eye algorithm has been extensively studied.
However, fish-eye lens optical transformation is complex
and different fish-eye lens have different designs. Hughes
et al.
[4,5]
have evaluated several fish-eye algorithms and
found that one algorithm could not fit all types of fish-
eyes lenses. However, previous work did not address
fish-eye lenses with FOV beyond 180
◦
. In this letter,
a circular fish-eye lens with a FOV of 186
◦
is used. We
adopt the surface projection model to derive the coor-
dinate transformation between the fish-eye image points
and their matching scene three-dimensional (3D) points
by orthogonal projection. Spherical projection model is
used in most applications
[6−9]
. However, for orthogonal
projection, the spherical projection model inherently lim-
its the FOV of the camera to 180
◦
. When the spherical
projection model is used to correct the 186
◦
fish-eye lens,
the corrected image is marked with barrel distortion. The
parabolic projection model prop osed by Wang et al. does
not have limitations of the spherical projection
[10]
. How-
ever, several pincushion distortions exist in the corrected
image of the parabolic projection.
According to the imaging theory of fish-eye lens, the
surface projection model can simulate the optical trans-
formation process. The corresponding relationship be-
tween the target points and the fish-eye image points
can be determined by the model, and the fish-eye images
can be corrected and transformed to normal plane per-
spective images.
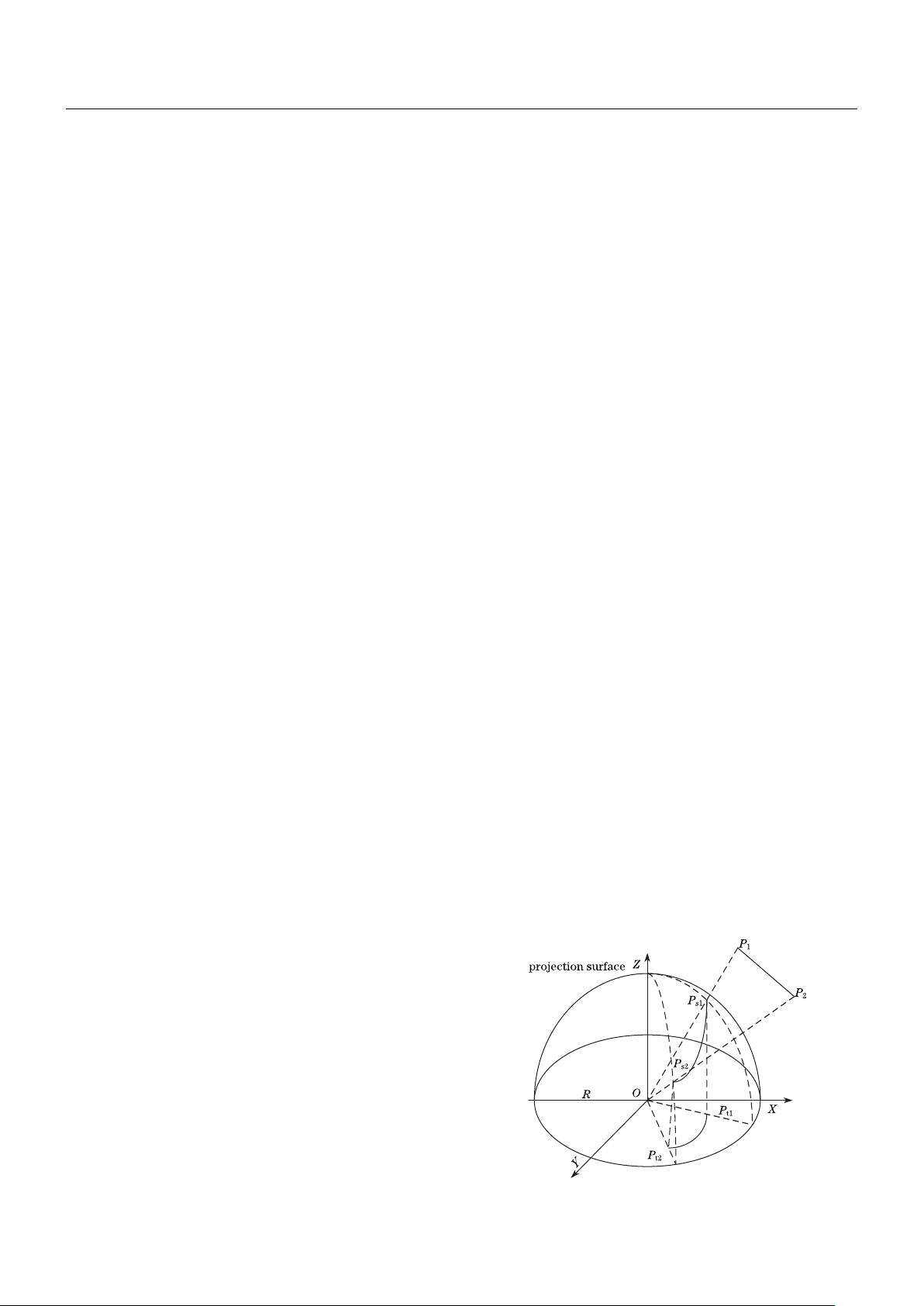
The rules of fish-eye surface projection model are
shown in Fig. 1. Suppose that the camera is at the
origin of coordinate O, shooting along the Z axis direc-
tion. The image taken by fish-eye lens is at the OXY
plane and fills a circular area. O is the center of the
fish-eye image outline and R is the radius. P
1
and P
2
are
the two points on the spatial line. P
s1
and P
s2
are the
two crossing points of OP
1
ray and OP
2
ray in relation
to the surface. Drawing lines perpendicular to the OXY
plane through the two points, we can obtain points P
t1
and P
t2
. P
t1
and P
t2
are the corresponding points in the
fish-eye imaging planes of P
1
and P
2
after the transfor-
mation of fish-eye lens. Straight lines are transformed to
curved lines by the fish-eye lens. The space coordinates
of P
1
are (X, Y, Z), the coordinates of P
t1
on the imag-
ing plane are (u, v), and the centers of the fish-eye image
outline O are (u
0
, v
0
). Consequently, the corresponding
relationship between the target points and the fish-eye
image points can be expressed as
(u − v
0
, v − v
0
) = D(X, Y, Z) , (1)
where D(X, Y, Z) represents the correction formula.
Previous studies have used the spherical projection
model to correct fish-eye images
[3−6]
. The projection
surface equation is expressed as
Fig. 1. Rules of fish-eye surface projection model.
1671-7694/2012/011002(4) 011002-1
c
° 2012 Chinese Optics Letters









