LIU et al.: FDM-STRUCTURED PREAMBLE OPTIMIZATION FOR CHANNEL ESTIMATION IN MIMO-OQAM/FBMC SYSTEMS 8435
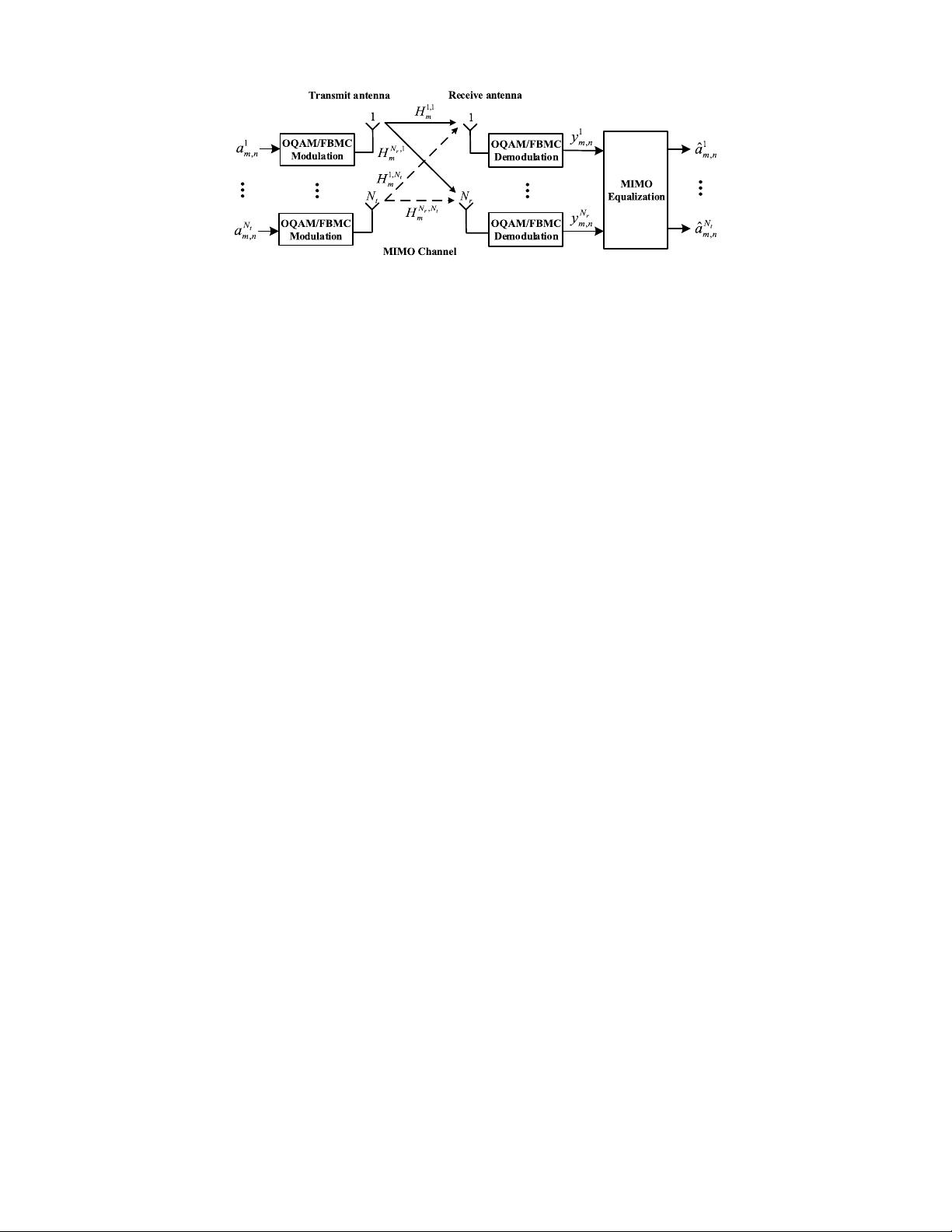
Fig. 1. The MIMO-OQAM/FBMC system model.
with ja
(i)
m,n
being the intrinsic imaginary interference from the
neighboring frequency-time (FT) points. With a well localized
pulse g[k] in time and frequency, it can be assumed that the
intrinsic imaginary interference mostly originates from the
first-order neighboring FT points [34]. Let us denote
ζ
p,q
m,n
=
∞
k=−∞
g
m,n
[k]g
∗
p,q
[k]. (3)
Then, the imaginary interference term ja
(i)
m,n
can be approxi-
mated as
ja
(i)
m,n
≈
(p
0
,q
0
)∈Ω
1
a
m+p
0
,n+q
0
ζ
m,n
m+p
0
,n+q
0
, (4)
where the neighborhood Ω
1
= {(p
0
,q
0
)| p
0
, q
0
∈{−1,
0, 1} and (p
0
,q
0
) =(0, 0)} and ζ
m,n
m+p
0
,n+q
0
represents the
contribution of a
m+p
0
,n+q
0
to the imaginary interference
ja
(i)
m,n
. It is noteworthy that for a well-designed prototype filter
g[k], ζ
m,n
m+p
0
,n+q
0
is pure imaginary for any (p
0
,q
0
) =(0, 0)
and ζ
m,n
m+p
0
,n+q
0
=1for (p
0
,q
0
)=(0, 0). Thus, for (p
0
,q
0
) =
(0, 0), in the remainder of this paper, we refer to the terms
ζ
m,n
m+p
0
,n+q
0
as the imaginary interference coefficients.
Note that, the intrinsic imaginary interference could be
removed by taking the real part after channel equalization.
In this paper, since we mainly focus on the preamble design
issues, the equalization and operation of taking real part are
not discussed.
B. MIMO-OQAM/FBMC System Model
The MIMO-OQAM/FBMC system model is depicted
in Fig. 1, where the transmitter and the receiver are equipped
with N
t
and N
r
antennas, respectively. Since the channel esti-
mation performance of MIMO-OQAM/FBMC systems would
not differ in the case of channel coding, we only consider the
uncoded scenario below.
At the transmitter side, the symbols spatially multiplexed
on the mth subcarrier at the nth time index are denoted by
a
m,n
=
a
1
m,n
,a
2
m,n
, ··· ,a
N
t
m,n
T
, each element of which
is transmitted at different antennas after the corresponding
OQAM/FBMC modulation. At the receiver side, the link
of each transmit and receive antenna pair is degraded by
multipath fading and contaminated with AWGN. For each
given FT position (m, n),letH
r,t
m
be the frequency response
of the channel between the tth transmit antenna and the rth
receive antenna and η
r
m,n
be the noise component at the
rth receive antenna. By assuming perfect time and frequency
synchronization, the demodulated symbol of the rth receive
antenna can be obtained by extending (2) to the MIMO case
as [16], [20]
y
r
m,n
=
N
t
t=1
H
r,t
m
c
t
m,n
+ η
r
m,n
, 1 ≤ r ≤ N
r
, (5)
where c
t
m,n
represents the corresponding virtually transmitted
symbol at the tth transmit antenna. According to (4), c
t
m,n
can
be written as
c
t
m,n
= a
t
m,n
+
(p
0
,q
0
)∈Ω
1
a
t
m+p
0
,n+q
0
ζ
m,n
m+p
0
,n+q
0
, 1 ≤ t ≤ N
t
.
(6)
We denote the demodulated symbol vector by y
m,n
=
y
1
m,n
,y
2
m,n
, ··· ,y
N
r
m,n
T
, the virtually transmitted vector by
c
m,n
=
c
1
m,n
,c
2
m,n
, ··· ,c
N
t
m,n
T
and the additive noise vector
by η
m,n
=
η
1
m,n
,η
2
m,n
, ··· ,η
N
r
m,n
T
. Thus, the equation (5)
can be expressed as
y
m,n
= H
m
c
m,n
+ η
m,n
, (7)
where
H
m
=
⎡
⎢
⎢
⎢
⎣
H
1,1
m
H
1,2
m
··· H
1,N
t
m
H
2,1
m
H
2,2
m
··· H
2,N
t
m
.
.
.
.
.
.
.
.
.
.
.
.
H
N
r
,1
m
H
N
r
,2
m
··· H
N
r
,N
t
m
⎤
⎥
⎥
⎥
⎦
(8)
is the MIMO channel frequency response (CFR) at that FT
point.
III. T
HE CONVENTIONAL PREAMBLE DESIGN METHODS
IN
MIMO-OQAM/FBMC SYSTEMS
Since the orthogonality condition of the OQAM/FBMC
system only holds in the real field, which causes intrinsic
imaginary interference to preamble symbols at the receiver,
preamble design in the OQAM/FBMC system is more difficult
than that in OFDM. Worse is that there also exists multi-
antenna interference when OQAM/FBMC is extended to the
MIMO case. In this section, we tackle the preamble design
problem in MIMO-OQAM/FBMC systems and give a brief
review of the conventional preamble design methods.
A. IAM Method
IAM preamble design method has drawn much attention
due to its simplicity and efficiency [20]. The IAM family
that includes IAM-R, IAM-imaginary (IAM-I), IAM-C, and
剩余10页未读，继续阅读
weixin_38538950
- 粉丝: 4
- 资源: 930
我的内容管理
展开
最新资源
- 李兴华Java基础教程：从入门到精通
- U盘与硬盘启动安装教程：从菜鸟到专家
- C++面试宝典：动态内存管理与继承解析
- C++ STL源码深度解析：专家级剖析与关键技术
- C/C++调用DOS命令实战指南
- 神经网络补偿的多传感器航迹融合技术
- GIS中的大地坐标系与椭球体解析
- 海思Hi3515 H.264编解码处理器用户手册
- Oracle基础练习题与解答
- 谷歌地球3D建筑筛选新流程详解
- CFO与CIO携手：数据管理与企业增值的战略
- Eclipse IDE基础教程：从入门到精通
- Shell脚本专家宝典：全面学习与资源指南
- Tomcat安装指南：附带JDK配置步骤
- NA3003A电子水准仪数据格式解析与转换研究
- 自动化专业英语词汇精华：必备术语集锦
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
