LCS-MMDPCA: 多批次工业过程在线监测的新方法

103 浏览量更新于2024-08-28 收藏 640KB PDF 举报

本文主要探讨了一种针对多批次复杂工业生产过程的在线监测方法，该方法名为"基于本地集合标准化和多模型动态主成分分析"（LCS-MMDPCA）。随着工业生产的复杂性和多样性，多个操作环节以及非高斯分布问题普遍存在，传统的统计模型可能无法有效应对这些挑战。首先，作者提出的方法认识到在实际生产环境中，由于操作人员的干预，各批次数据的统计特性可能并不遵循正态分布，这是构建多变量统计模型的一大难题。为了克服这个问题，研究人员设计了一个创新的解决方案。他们将复杂的多批次生产过程分解为一系列阶段，每个阶段代表一个操作环节。这样做的目的是将复杂的流程简化，便于处理和分析。在每个阶段内，数据被进一步进行本地集合标准化处理，这是一种预处理技术，它能够确保数据在各个维度上具有相同的尺度和分布，从而减少非正态性的影响。这种标准化有助于提高后续分析的稳健性和有效性，使得即使面对非高斯分布的数据，也能更好地提取其内在结构。接着，研究人员采用多模型动态主成分分析（MMDPCA）来对各阶段内的数据进行降维和特征提取。MMDPCA是一种结合了多种模型优势的动态方法，它能够在不同的操作阶段捕捉到数据的不同特征模式，同时考虑到数据随时间的变化。通过这种方式，该方法能够有效地捕捉到生产过程中各批次间的动态变化，提高了监测的实时性和准确性。这篇研究论文提出了一种新颖的在线监测策略，它巧妙地结合了本地集合标准化和多模型动态主成分分析，旨在解决多批次生产过程中的非高斯分布和多操作问题。这种方法通过分解、标准化和动态建模，不仅适应了工业生产环境的复杂性，还提升了生产过程的在线监控性能，对于提升制造业的效率和质量控制具有重要的实践价值。

methods such as partitioning, hierarchical, and density-based

methods. Since the hierarchical clustering

[30,31]

is a class of

simple high-dimensional and high efﬁciency methods, it is

adopted in this paper for automatically partitioning the operations

into several clusters. For multi-operation processes, the changes of

set values can be used to indicate the changes in the operation.

Hence, hierarchical clustering is implemented according to the

similarity of set values.

The similarity of set values between batches is deﬁned as

follows:

gðS

; S

Þ¼1 

 S

¼ 1 

j¼1

i;j

 S

k;j

; i; k ¼ 1; I

where S

and S

are set values matrices of the ith and kth batches;

i;j

and S

k;j

are the set values of the jth variable of S

and S

i;k

2½0;1. More variable g

i;k

means greater similarity between

batch data.

The hierarchical clustering method is used according to g

i;k

;

special algorithm is as follows:

(1) Calculate the similarity g

i;k

between every two batches and

ﬁnd the two batches with the maximum g, and then merge

these two batches as a cluster.

(2) Calculate the average set value of the merged batches data

and calculate the similarity g between batches or clusters;

ﬁnd the batches or the clusters with the maximum g and then

merge the batches or the clusters as a new cluster.

(3) Repeat step (2) until g < a, a is the similarity threshold.

The threshold a (0 < a < 1) determines the accuracy and

complexity of the developed cluster-based sub-model. Obviously,

small a values result in coarse clustering and less accurate

modelling, whereas large a values can improve modelling accuracy

but need more sub-models and increase the modelling complexity.

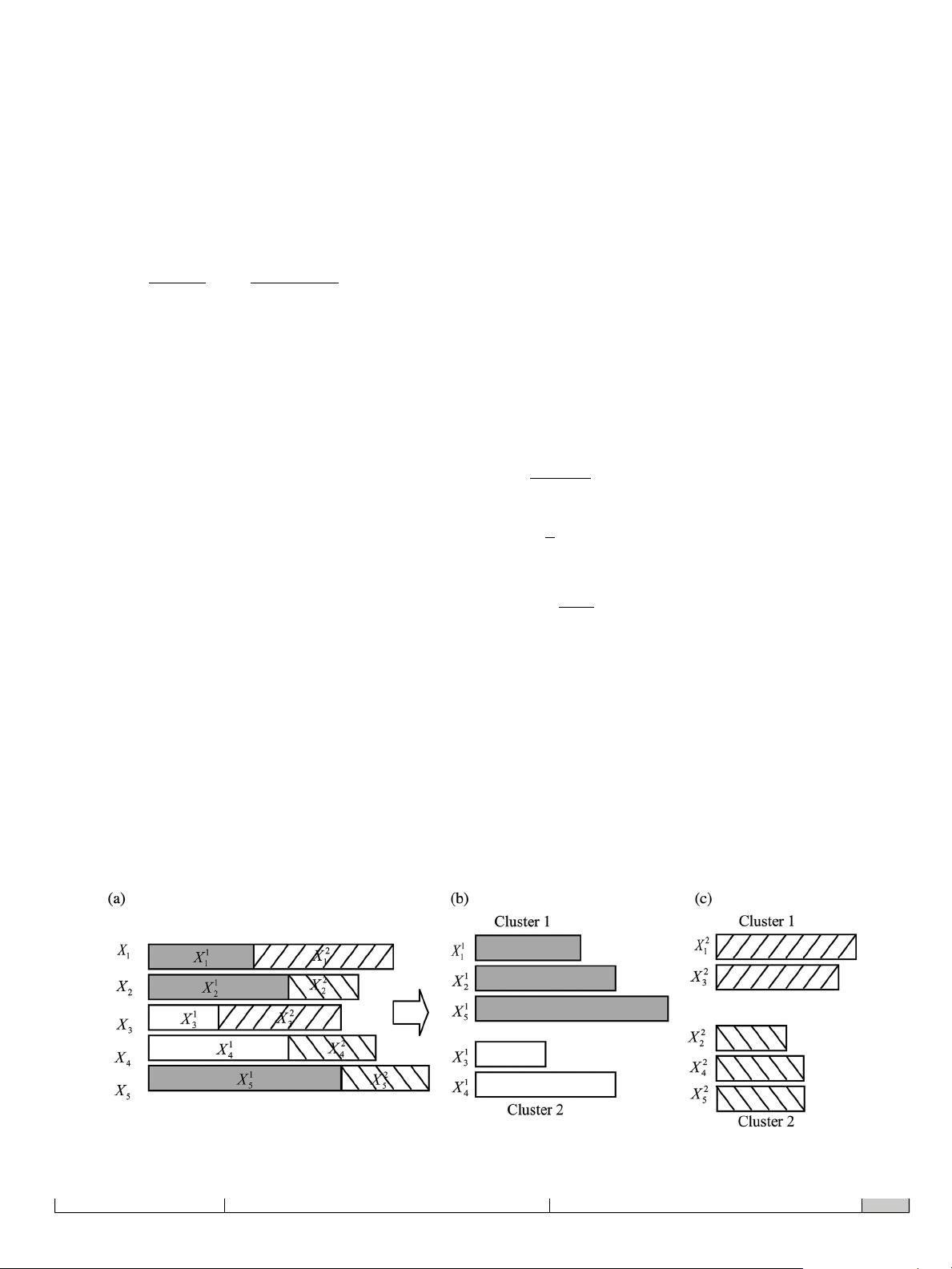
To facilitate understanding, we illustrate the clustering process

with Figure 1. Assume that there are 5 batch data and the number

of stages is 2 for each batch. The data with the same colour and

drawing indicates that set values of these batches are similar, thus

the data can be clustered together by the hierarchical clustering

method. In Figure 1, the number of clusters is 2 for each stage,

where subscript X indicates batch index, and superscript X

indicates stage index. The data belonging to the same cluster show

that their set values are in the same range.

Data Preprocessing

For a batch process, the data used for modelling is a three-way

matrix XðI  J  K

Þ; i=1; 2; ; I: where I is the number of

reference batches, J is the number of selected process variables,

and K

is the number of samples in each batch. As aforementioned,

the duration K

is different between batches. The data belonging to

the same cluster are designated as X

ðI

 J  K

Þ, where I

is the

number of batches belonging to the same cluster, K

is the number

of samples in batch i, i ¼ 1,2,..., I

. In real industrial processes,

since the sequence of operating steps is quite complex and almost

non-reproducible, no attempts are conducted to synchronize the

time evolution of the batch. The three-way matrix is therefore

unfolded into a bi-dimensional array, designated as X

 JðÞ,

by a variable-wise technique.

[32]

Since a series of manual

operations make the bi-dimensional array data follow non-

Gaussian distribution, the array data should be pre-processed.

For most MSPM methods, the batch data often need to be

normalized by z-score method before modelling. The standardized

method can normalize each variable to the same level with zero

mean and unit variance. For a training dataset X 2 R

KJ

, K is the

number of samples and J is the number of process variables, the

normalizing process of the z-score method is expressed as follows:

 EðXÞ

SðXÞ

; n ¼ 1; 2; ; K ð3Þ

EðXÞ¼

n¼1

ð4Þ

SðXÞ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

K  1

n¼1

ðx

 EðXÞÞ

ð5Þ

where x

is a sample in training dataset, E(X) represents the mean

vector, and S(X ) is the standard deviation vector. The z-score

method is valid to normalize each variable to the same level when

the training data obey Gaussian distribution. However, it will

cause some problems when the z-score method is used for multi-

operation data. Since constant mean and standard deviation

computed from the entire dataset are used in the z-score method,

when the operation is changed, the standard deviation is likely to

change dramatically because the mean of the dataset might be

changed largely. The dataset might still follow non-Gaussian

distribution after z-score. To make the data in multi-operation

Figure 1. Cluster process: (a) original data, (b) in the ﬁrst stage, and (c) in the second stage.

VOLUME 94, OCTOBER 2016 THE CANADIAN JOURNAL OF CHEMICAL ENGINEERING

1967

剩余11页未读，继续阅读

weixin_38611508

粉丝: 1
资源: 884

LCS-MMDPCA: 多批次工业过程在线监测的新方法

动态多核PCA在工业生产过程性能监测中的有效策略

基于批次加权软划分的多阶段AR-PCA间歇过程监测

多阶段动态PCA在发酵故障监测中的应用

基于多阶段动态PCA的发酵过程故障监测 (2012年)

基于分布式ICA-PCA模型的工业过程故障监测.pdf

基于多动态核 PCA的统计过程监测策略研究 (2012年)

MyPCA.rar_avoidy53_pca_pca监测_过程监测

基于故障子空间与PCA监测模型的故障可检测性研究

基于MICA-PCA的间歇过程故障监测 (2014年)

基于迭代PCA的在线过程监测：有效性和可行性研究

最新资源