Transformer基的可扩展扩散模型

需积分: 5 89 浏览量更新于2024-06-14 收藏 41.8MB PDF 举报

"Scalable Diffusion Models with Transformers" 本文探讨了一种基于Transformer架构的新一类扩散模型。传统的图像扩散模型通常采用U-Net作为基础结构，而作者则将这一结构替换为处理潜在补丁的Transformer，从而构建了所谓的Diffusion Transformers（DiTs）。他们通过分析前向传递的复杂性（以Gflops为衡量标准）来研究DiTs的可扩展性。研究发现，具有更高Gflops的DiT（通过增加Transformer的深度、宽度或输入令牌的数量）在FID（Fréchet Inception Distance）指标上持续表现更优。 1. 引言机器学习领域正在经历快速发展，尤其是在生成模型方面。扩散模型作为一种生成式模型，已经在图像生成任务中取得了显著的成果。然而，如何实现这些模型的高效和可扩展性是当前面临的挑战。Transformer自其在自然语言处理领域的成功应用以来，逐渐被引入到计算机视觉任务中，因其并行计算能力和对全局信息的捕捉能力而受到关注。 2. 方法本文提出的Diffusion Transformers（DiTs）利用Transformer的特性，能够在潜在空间中对图像进行建模。与U-Net相比，Transformer可以在更大的输入尺寸上进行操作，并且可以更有效地处理全局依赖关系。通过将图像分割成小块（补丁），Transformer能够并行处理这些局部信息，从而提高了计算效率。 3. 实验与结果实验部分，作者训练了不同规模的DiT模型，包括在ImageNet数据集上训练的DiT-XL/2模型，分别在512x512和256x256分辨率下进行。结果显示，随着模型复杂度的增加，即Gflops的增加，DiT的FID分数（评估生成图像质量的指标）显著降低。其中，最大的DiT-XL/2模型在类条件的ImageNet 512x512和256x256基准测试中，达到了最先进的FID成绩，256x256分辨率下的FID仅为2.27，这表明了模型的出色性能。 4. 讨论与未来工作尽管DiTs展示了出色的性能和可扩展性，但其仍然存在计算资源的需求较高和训练时间较长的问题。未来的研究方向可能包括优化Transformer的结构以减少计算需求，或者探索更有效的训练策略以缩短训练时间。此外，将DiTs应用于其他领域，如视频生成或3D对象建模，也可能成为研究的焦点。 “Scalable Diffusion Models with Transformers”通过将Transformer引入扩散模型，实现了模型在生成图像质量上的新高度，并提供了良好的可扩展性，为未来高效率、高质量的生成模型设计提供了新的思路。

100K 200K 300K 400K

Training Steps

100

FID-50K

XL/2 In-Context

XL/2 Cross-Attention

XL/2 adaLN

XL/2 adaLN-Zero

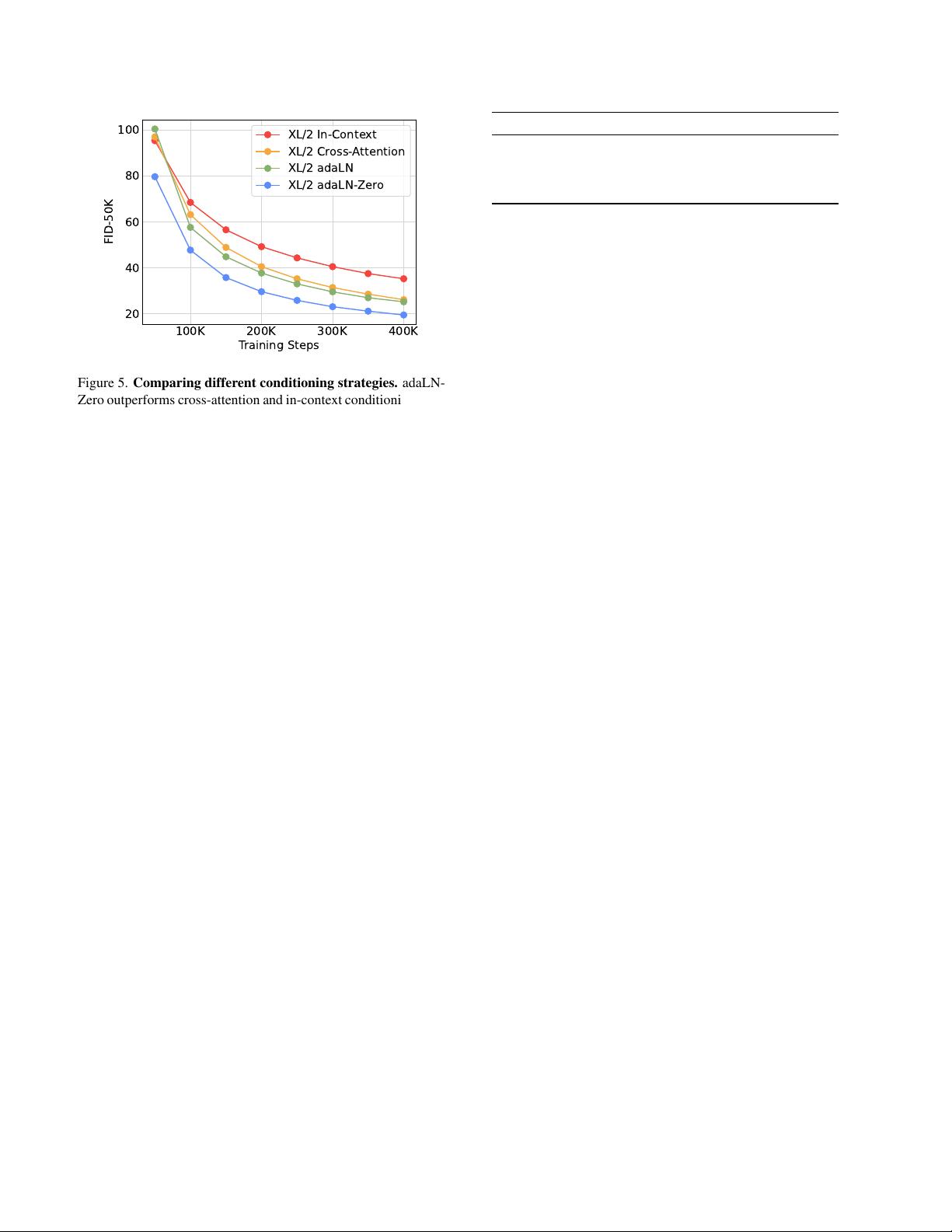
Figure 5. Comparing different conditioning strategies. adaLN-

Zero outperforms cross-attention and in-context conditioning at all

stages of training.

– Cross-attention block. We concatenate the embeddings

of t and c into a length-two sequence, separate from

the image token sequence. The transformer block is

modiﬁed to include an additional multi-head cross-

attention layer following the multi-head self-attention

block, similar to the original design from Vaswani et

al. [60], and also similar to the one used by LDM for

conditioning on class labels. Cross-attention adds the

most Gﬂops to the model, roughly a 15% overhead.

– Adaptive layer norm (adaLN) block. Following

the widespread usage of adaptive normalization lay-

ers [40] in GANs [2, 28] and diffusion models with U-

Net backbones [9], we explore replacing standard layer

norm layers in transformer blocks with adaptive layer

norm (adaLN). Rather than directly learn dimension-

wise scale and shift parameters γ and β, we regress

them from the sum of the embedding vectors of t and

c. Of the three block designs we explore, adaLN adds

the least Gﬂops and is thus the most compute-efﬁcient.

It is also the only conditioning mechanism that is re-

stricted to apply the same function to all tokens.

– adaLN-Zero block. Prior work on ResNets has found

that initializing each residual block as the identity

function is beneﬁcial. For example, Goyal et al. found

that zero-initializing the ﬁnal batch norm scale factor γ

in each block accelerates large-scale training in the su-

pervised learning setting [13]. Diffusion U-Net mod-

els use a similar initialization strategy, zero-initializing

the ﬁnal convolutional layer in each block prior to any

residual connections. We explore a modiﬁcation of

the adaLN DiT block which does the same. In addi-

tion to regressing γ and β, we also regress dimension-

wise scaling parameters α that are applied immediately

prior to any residual connections within the DiT block.

Model Layers N Hidden size d Heads Gﬂops (I=32, p=4)

DiT-S 12 384 6 1.4

DiT-B 12 768 12 5.6

DiT-L 24 1024 16 19.7

DiT-XL 28 1152 16 29.1

Table 1. Details of DiT models. We follow ViT [10] model con-

ﬁgurations for the Small (S), Base (B) and Large (L) variants; we

also introduce an XLarge (XL) conﬁg as our largest model.

We initialize the MLP to output the zero-vector for all

α; this initializes the full DiT block as the identity

function. As with the vanilla adaLN block, adaLN-

Zero adds negligible Gﬂops to the model.

We include the in-context, cross-attention, adaptive layer

norm and adaLN-Zero blocks in the DiT design space.

Model size. We apply a sequence of N DiT blocks, each

operating at the hidden dimension size d. Following ViT,

we use standard transformer conﬁgs that jointly scale N,

d and attention heads [10, 63]. Speciﬁcally, we use four

conﬁgs: DiT-S, DiT-B, DiT-L and DiT-XL. They cover a

wide range of model sizes and ﬂop allocations, from 0.3

to 118.6 Gﬂops, allowing us to gauge scaling performance.

Table 1 gives details of the conﬁgs.

We add B, S, L and XL conﬁgs to the DiT design space.

Transformer decoder. After the ﬁnal DiT block, we need

to decode our sequence of image tokens into an output noise

prediction and an output diagonal covariance prediction.

Both of these outputs have shape equal to the original spa-

tial input. We use a standard linear decoder to do this; we

apply the ﬁnal layer norm (adaptive if using adaLN) and lin-

early decode each token into a p×p×2C tensor, where C is

the number of channels in the spatial input to DiT. Finally,

we rearrange the decoded tokens into their original spatial

layout to get the predicted noise and covariance.

The complete DiT design space we explore is patch size,

transformer block architecture and model size.

4. Experimental Setup

We explore the DiT design space and study the scaling

properties of our model class. Our models are named ac-

cording to their conﬁgs and latent patch sizes p; for exam-

ple, DiT-XL/2 refers to the XLarge conﬁg and p = 2.

Training. We train class-conditional latent DiT models at

256 × 256 and 512 × 512 image resolution on the Ima-

geNet dataset [31], a highly-competitive generative mod-

eling benchmark. We initialize the ﬁnal linear layer with

zeros and otherwise use standard weight initialization tech-

niques from ViT. We train all models with AdamW [29,33].

剩余24页未读，继续阅读

muyu_525

粉丝: 2
资源: 19

Transformer基的可扩展扩散模型

sora学习文档集合三

Scalable Parallel Programming with CUDA中文版

激光SLAM Hector官方论文A Flexible and Scalable SLAM System with Full1

如何设计一个基于Transformer架构的扩散模型来提升图像生成质量，并确保模型的可扩展性？

stable diffusion model size

highly-scalable searchable symmetric encryption with support for boolean que

nodejs+express+mongoose

xapp1317-scalable-matrix-inverse-hls

plc for next

Deep Learning Toolbox

最新资源