回归分析中的定性变量赋值与哑变量处理

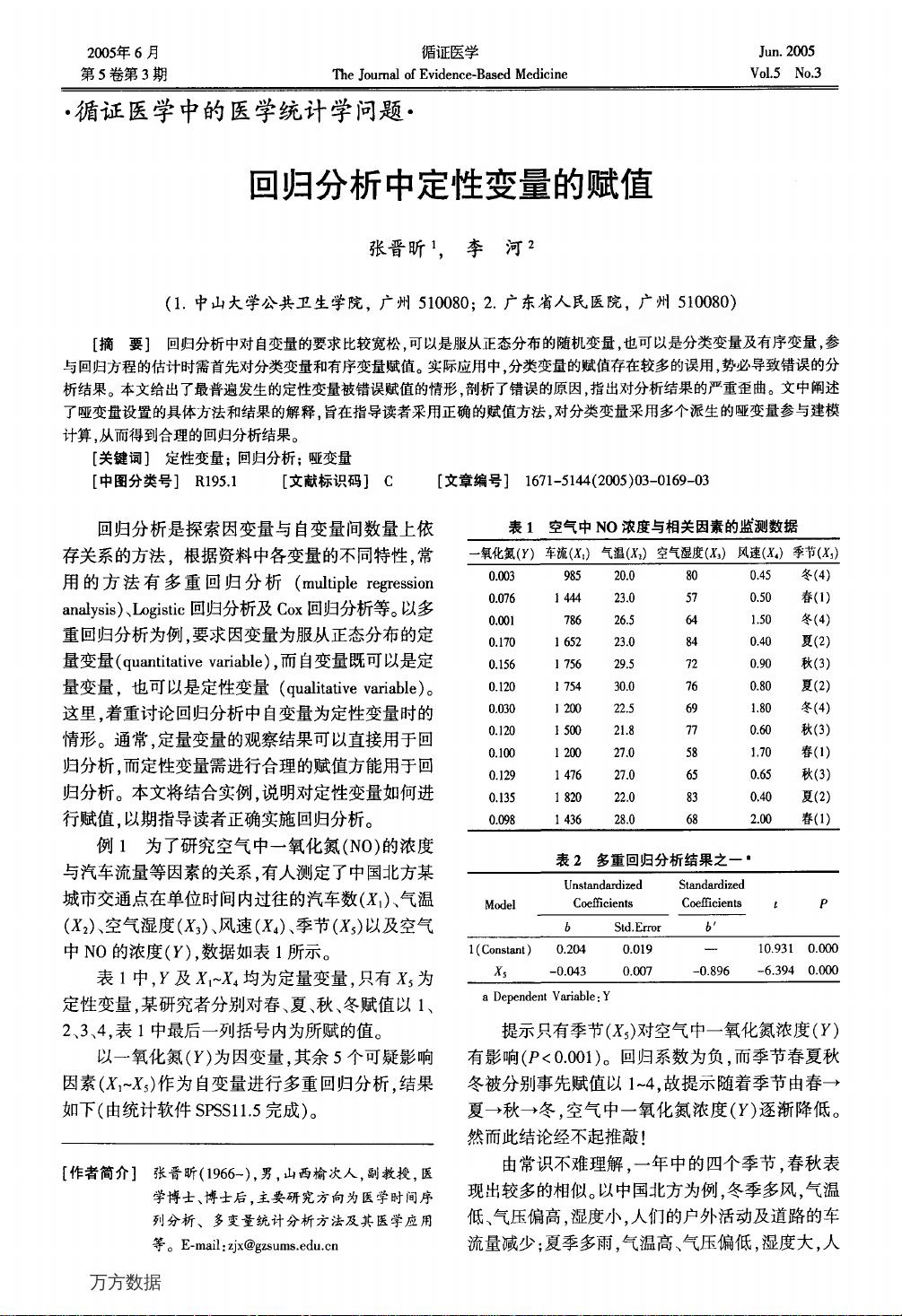
"回归分析是探索因变量与自变量间数量上依存关系的方法，涉及数学建模中的变量赋值问题。在回归分析中，自变量可以是定量或定性，但定性变量需要合理赋值才能进行分析。错误的赋值会导致分析结果的歪曲。哑变量设置是处理定性变量常用的方法，通过创建多个派生的哑变量来代表不同的类别，使得定性变量能够参与建模计算。" 回归分析是一种统计技术，用来分析因变量（目标变量）与一个或多个自变量（解释变量）之间的关系。在数学建模中，特别是涉及回归分析时，变量的赋值是一个关键步骤。自变量可以是连续的定量变量，也可以是离散的定性变量。对于定量变量，其观测值可以直接用于分析；但对于定性变量，如分类变量，需要转换为数值形式才能纳入模型。 例如，在一个研究中，可能要分析空气质量与汽车流量、气温、湿度、风速等因素的关系，其中“季节”是一个定性变量。如果简单地给春季、夏季、秋季和冬季赋予数值1、2、3、4，这种赋值方式可能导致误导性的分析结果，因为这实际上暗示了季节之间存在序数关系，而事实上季节的顺序并不意味着影响的强度。 正确处理定性变量的方式是使用哑变量（也称为虚拟变量）。对于每个类别，创建一个新变量，仅在该类别出现时取值1，其他情况取值0。例如，对于“季节”，可以创建四个哑变量：Spring、Summer、Autumn和Winter。如果某个观测属于春季，那么Spring变量取1，其他三个取0；如果属于夏季，Summer取1，其余取0，以此类推。这种方法确保了每个定性变量的类别都被独立地考虑，不会引入不适当的顺序或等级信息。 在回归分析中，这些哑变量会与因变量一起纳入模型，帮助我们理解不同类别对因变量的影响。每个哑变量的系数表示相对于参照类别的效应大小。例如，如果夏季的系数大于春季，这表示夏季相对于春季，空气中一氧化氮的浓度有更显著的变化。 正确地对定性变量进行赋值是进行有效回归分析的关键，尤其是在涉及定性因素的复杂模型中。哑变量的使用提供了一种量化定性信息的方法，使得统计模型能够处理非数值数据，从而得出更准确的结论。在实际应用中，需要根据研究目的和数据特性，选择合适的变量赋值策略，避免因错误处理而导致的分析偏差。