数字信号处理MATLAB作业：抽样频率与循环卷积实例

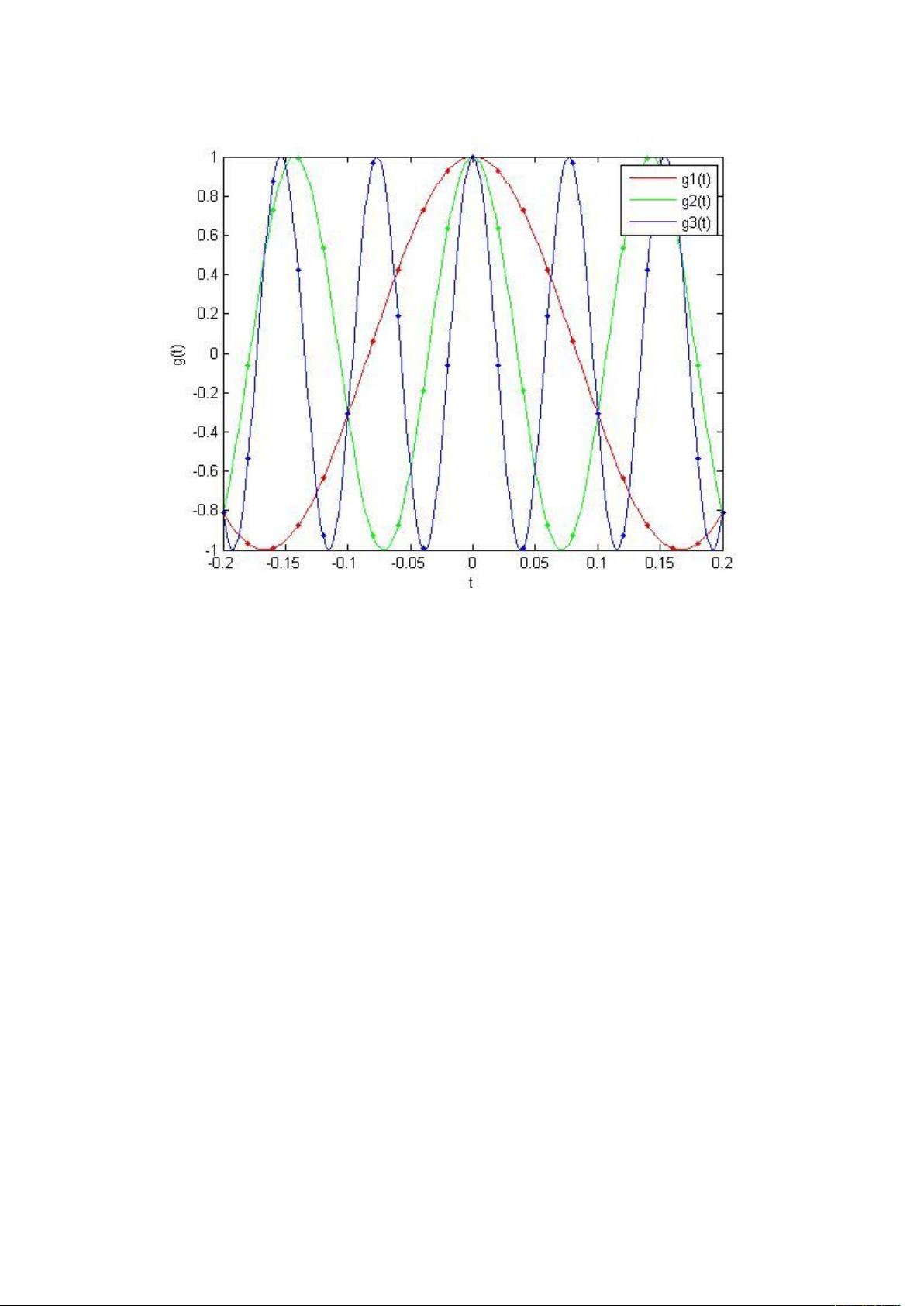
在本篇文档中，主要探讨的是数字信号处理课程中的MATLAB作业，涉及到信号采样与重构以及离散傅立叶变换(DFT)的应用。以下是两个具体问题的详细解析： M1-1 该部分主要关注抽样定理在数字信号处理中的应用。题目要求对三个不同周期的余弦函数（，，）进行抽样，并用MATLAB进行可视化。原始函数的抽样频率过低导致抽样点虽相同，但重构后的信号并不准确。通过将抽样频率从原来的增加到50Hz，可以观察到抽样点的值与原函数值更加接近，从而更好地还原信号。程序代码展示了如何绘制抽样点和原始信号，以及使用subplot进行分层展示。同时，通过改变抽样频率，学生可以理解抽样定理的重要性，即为了正确重建连续信号，抽样频率应大于信号最高频率的两倍。 M2-1 这个任务涉及到了离散傅立叶变换(DFT)在计算序列循环卷积中的应用。具体步骤包括定义两个序列（g[k] 和 h[k]），其中g[k] = {1, -3, 4, 2, 0, -2} 和 h[k] = {3, 0, 1, -1, 2, 1}，以及另一个序列x[k] = cos(k/2) 和 y[k] = 3k。循环卷积是信号处理中的一个重要概念，它表示两个序列经过多次平移并求和的结果。对于第一个序列的循环卷积，通过调用fft函数计算两个序列的离散傅立叶变换，然后进行点乘，再通过ifft函数进行逆变换得到结果。代码中的for循环用于迭代计算卷积的各个元素。 总结来说，这个MATLAB作业涵盖了数字信号处理的基础理论，如抽样定理、离散傅立叶变换及其在信号分析和处理中的应用。通过这些习题，学生能够掌握如何使用MATLAB工具进行信号采样与重构，以及如何运用DFT进行频域分析和卷积运算，这对于深入理解信号处理的原理和实践操作具有重要意义。