KMP算法详解：无公式理解与实战应用

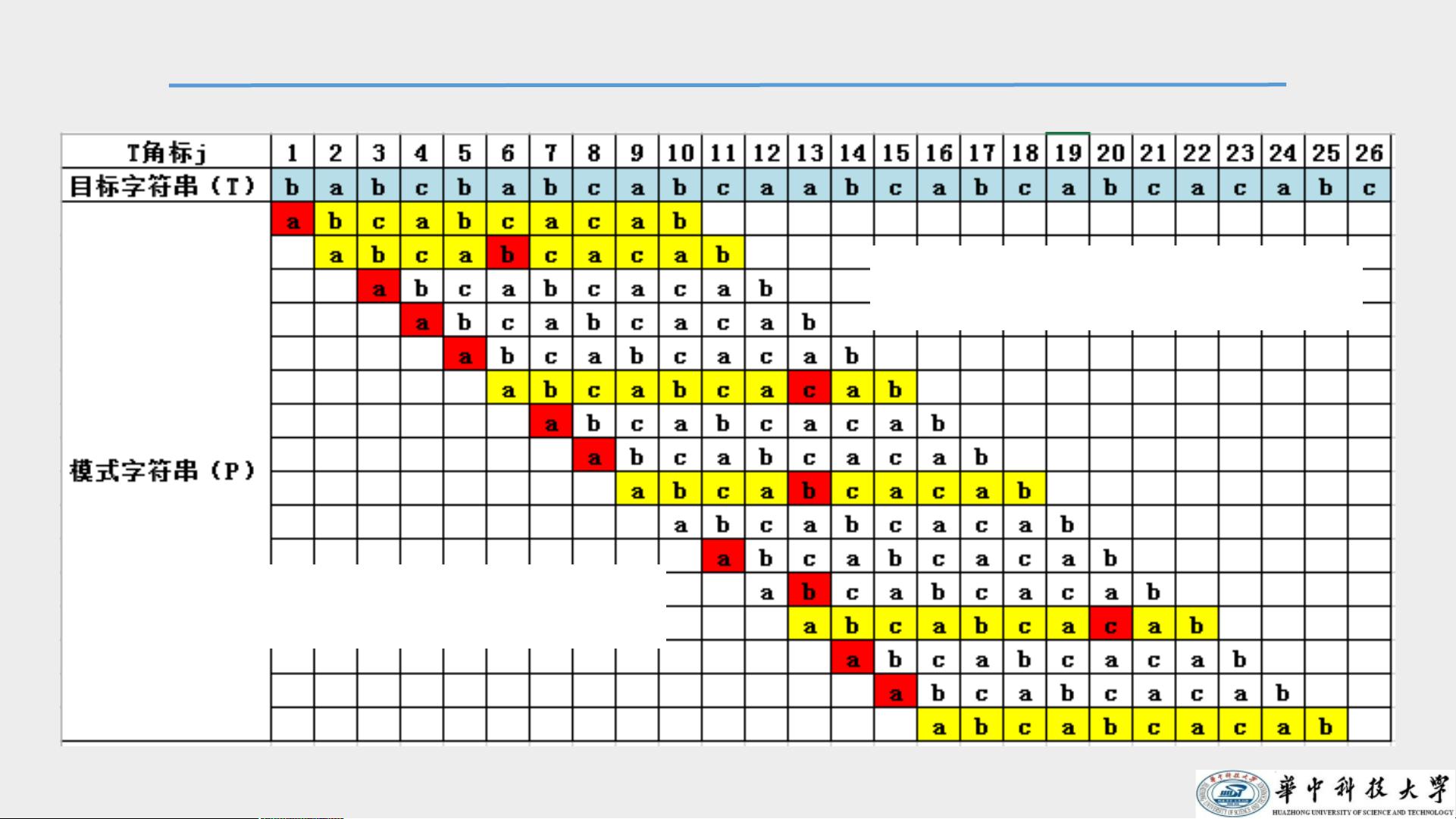
KMP算法是一种高效的字符串匹配算法，由Donald Knuth、James Morris和Vint Cerf的缩写KMP共同命名，它在寻找模式串在目标串中的位置时，能够在线性时间内完成，避免了朴素匹配中的重复搜索，从而大大提高查找效率。KMP算法的核心在于跳转表next[]的设计，它解决了模式串的前缀包含问题。 在朴素匹配中，为了查找模式串P=abcabcacab在目标串T=babcbabcabcaabcabcabcacabc中的所有出现，我们需要逐个字符比对，导致时间复杂度为O(m*n)，其中m为模式串长度，n为目标串长度。而KMP算法通过预处理模式串，构建了next[]数组，这个数组存储了模式串中每个位置的最长公共前后缀长度。例如，对于模式串P，其next[]数组为[0, 0, 1, 2, 0, 0, 0, 3, 0, 0, 1]，这意味着如果在匹配过程中遇到失败，可以根据next[]数组确定模式串应向后移动多少个字符，从而跳过已经匹配过的部分。 当我们在匹配过程中遇到第一个不匹配的情况，例如在第8个字符位置，如果模式串中的'a'不等于目标串中的'c'，朴素匹配会回溯到上一个字符，而KMP算法则利用next[]得知应向后移动5个字符，即跳到第3个字符继续匹配。这种跳跃的方式减少了不必要的比较，使得整个匹配过程更加高效。 KMP算法的关键步骤如下： 1. **构造next[]**：根据模式串的前缀和后缀的相同部分计算next[]，确保在匹配失败时能够跳过已匹配的部分，而不是每次都回溯到上一个字符。 2. **匹配过程**：从目标串的第一个字符开始，逐个与模式串的字符比较，当匹配失败时，根据next[]数组决定模式串的移动位置。 3. **优化性能**：KMP算法的时间复杂度为O(n)，其中n为目标串长度，这意味着它具有线性的平均和最坏情况时间复杂度，大大优于朴素匹配的O(m*n)。 通过理解并应用KMP算法，无论是文本编辑中的关键词查找，还是在网络协议解析等场景中，都能够显著提升字符串匹配的效率，因此KMP算法在计算机科学领域具有重要的实用价值。