线性代数基础：向量与线性组合解析

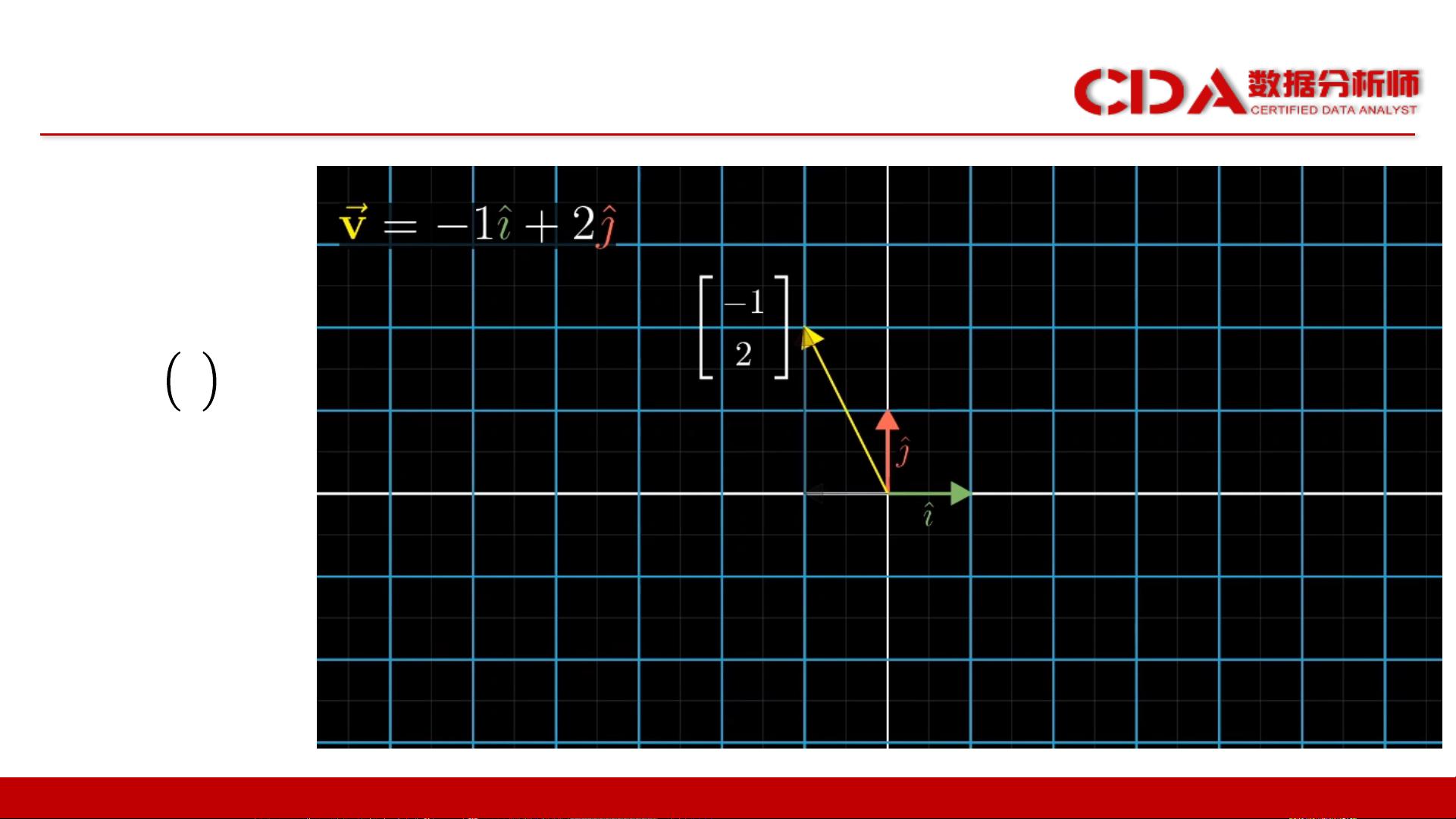
"这是一份线性代数的基础教程，特别适合那些正在学习数据分析并希望强化线性代数基础知识的人。课程由CDA数据分析师提供，具有严谨的课程体系、专业的师资团队和优质的教学服务。内容涵盖了向量、向量运算、线性组合等关键概念，旨在帮助学习者更好地理解和应用线性代数于数据分析领域。" 线性代数是现代数学和数据分析的重要基石，特别是在处理高维数据和复杂统计模型时。这个培训课件主要讲解了以下几个核心知识点： 1. **向量**：向量是具有大小和方向的量，可以用来表示物理中的力、统计学中的趋势或计算机中的数据点。在数学中，向量通常由一对有序数字（如坐标）表示，描述它在二维空间中的位置。向量的起点可以被假设为原点，而终点则表示向量的方向和长度。 2. **向量运算**：包括向量的加法和数乘。向量加法是通过将两个向量的对应分量相加形成新向量，形成一个平行四边形的对角线。数乘向量则是对向量进行缩放，正数表示同向放大，负数表示反向放大。 3. **线性组合**：任何向量都可以表示为一组基向量的线性组合，也就是基向量的标量乘积之和。单位向量是长度为1的向量，通常作为坐标系的基向量，而零向量表示没有任何方向和长度的向量。 4. **基向量与基组**：基向量是定义向量空间的基本元素，它们的线性组合可以表示空间中的任何向量。一个基组包含足够数量的线性无关向量，使得所有其他向量都能由这些基向量唯一表示。 5. **张量与子空间**：在二维空间中，两个非零向量的线性组合可以形成一个平面，除非这两个向量共线，此时只能形成一条直线。张量是更高维度的向量概念，而由向量的线性组合形成的子空间是向量空间的一部分，具有自身的线性结构。 学习线性代数对于理解数据分析中的多元统计方法，如线性回归、主成分分析和奇异值分解等至关重要。它提供了描述和操作复杂数据集的工具，帮助我们在高维空间中进行有效的建模和推断。对于CDA数据分析师的学习者而言，这份课件将为他们在数据分析领域奠定坚实的基础。