Python构建霍夫曼树：最小带权路径长度与应用

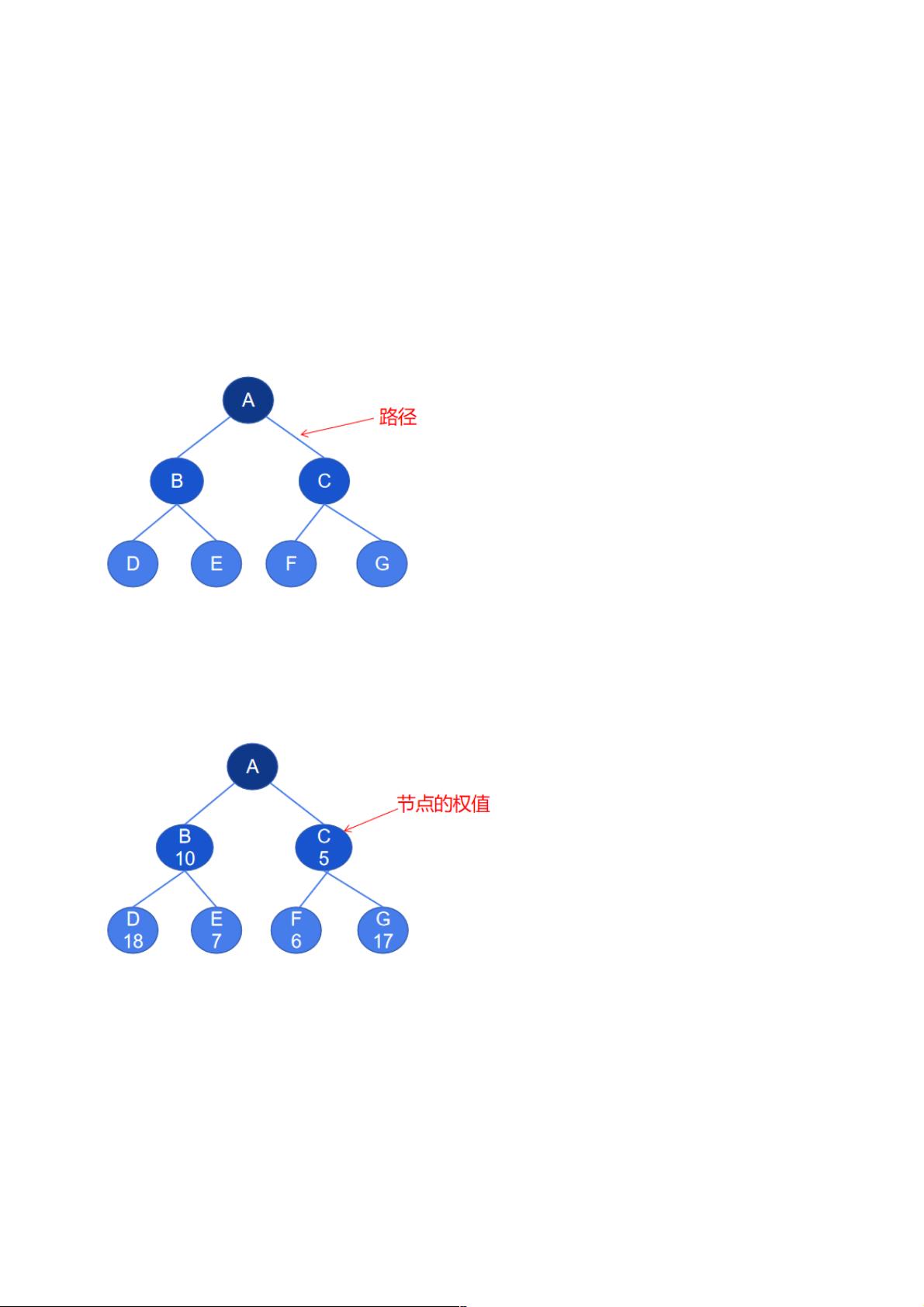
"Python实现霍夫曼树" 霍夫曼树是一种高效的、用于数据编码和压缩的特殊二叉树。它的核心特点是带权路径长度最短，即从根节点到所有叶节点的路径长度乘以其相应的权值之和最小。这种特性使得霍夫曼树在数据压缩领域具有广泛应用，例如在文本压缩、图像压缩等场景中。 霍夫曼树构建的基本步骤如下： 1. **创建最小堆**：将给定的N个权值视为N个初始的、只有一个节点的霍夫曼树（这些节点称为叶节点），并将其放入一个优先队列（通常用最小堆实现）中，按照权值大小排序。 2. **合并最小节点**：每次从堆中取出两个权值最小的节点，将它们合并成一个新的内部节点，该节点的权值是两个子节点权值之和。新节点有两个子节点，分别是取出的两个节点。然后将这个新节点放回堆中。 3. **重复步骤2**：继续这个过程，直到堆中只剩下一个节点，这个节点就是霍夫曼树的根节点。 这个过程中，权值较大的节点会更快地向树的顶部移动，因为在每次合并时，都会选择权值最小的节点。最终形成的树就是带权路径长度最小的霍夫曼树。 在Python中实现霍夫曼树，可以使用`heapq`库来创建和管理最小堆。首先，需要定义一个`HuffmanNode`类来表示树的节点，包括权值、左子节点和右子节点。接着，实现一个函数来创建霍夫曼树，该函数接收一个包含权值的列表，使用堆来构造树，并返回根节点。最后，可以通过遍历霍夫曼树来生成霍夫曼编码，这通常是一个二进制编码，其中权值小的节点对应的编码是0，权值大的节点对应的编码是1。 在应用霍夫曼编码时，先通过霍夫曼树生成每个字符或符号的编码，然后将源数据按照编码转换，从而实现数据压缩。解压缩时，根据编码表反向解析二进制数据，恢复原信息。 需要注意的是，霍夫曼树并非唯一，给定相同的权值集，可能会有多种不同的霍夫曼树结构，但其带权路径长度应当相同。在实际应用中，我们通常只关心最小带权路径长度的霍夫曼树。 Python实现霍夫曼树的关键在于理解和运用优先队列（最小堆）来构建最优二叉树，并利用这个树进行数据的编码和压缩。通过对霍夫曼树的深入理解，我们可以更好地设计和优化数据压缩算法，提高存储和传输效率。