T检验:小样本均值差异显著性检验
需积分: 50 29 浏览量
更新于2024-09-01
2
收藏 413KB DOCX 举报
"T检验入门.docx"
T检验是统计学中一种重要的假设检验方法,尤其适用于处理样本量较小(通常n<30)且总体标准差未知的情况。它由戈斯特在1908年提出,最初是为了评估酿酒的质量,由于商业机密原因,戈斯特以笔名"学生"发表了这一成果,因此T检验也被称为Student's t检验。
T检验的核心目的是判断两个独立或配对样本的均值之间是否存在显著差异。在实际应用中,例如"超级引擎"工厂的案例,我们需要验证新生产的引擎排放量均值是否低于政府规定的20ppm。传统的做法是测量所有引擎的排放值并计算平均值,但随着工厂产量的增加,这种做法变得不切实际。
为了解决这个问题,我们可以采用T检验的思路:首先设定原假设(H0)和备择假设(H1)。在本例中,原假设是μ⩾20,即引擎排放均值不小于20ppm;备择假设是μ<20,表示排放均值小于20ppm。接着,我们随机抽取一部分样本(例如10台引擎)进行测量,并计算这些样本的平均值。由于样本数量小且总体标准差未知,我们将使用t统计量来评估结果。
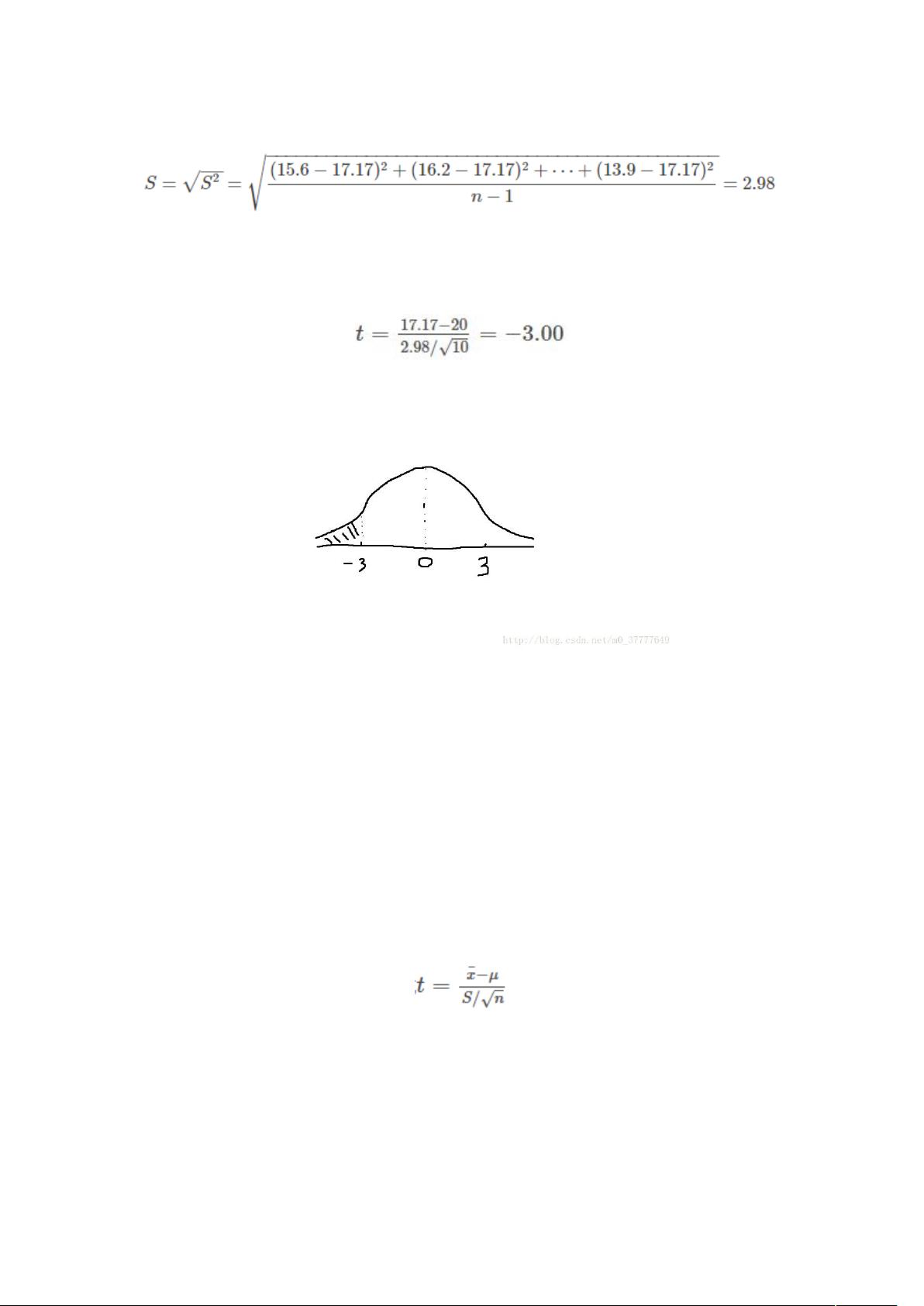
t统计量是一个基于样本数据计算出的标准化值,它反映了样本均值与总体均值之间的差异相对于样本波动性的大小。对于小样本,t统计量的分布遵循t分布,其形状依赖于样本大小和总体方差。计算t统计量的公式如下:
t = (样本均值 - 假设均值) / (样本标准差 / √样本大小)
在确定了t统计量后,我们可以查t分布表或使用统计软件计算对应的p值。p值表示在原假设成立的情况下,观察到当前样本或更极端样本结果的概率。若p值小于预设的显著性水平(通常为0.05或0.01),则拒绝原假设,认为样本间存在显著差异;若p值大于显著性水平,保留原假设,表示差异可能由随机性造成,不具统计意义。
总结来说,T检验提供了一种有效的方法,通过小样本数据来推断总体间的差异,特别适合在总体参数未知且样本量较小的情况下进行数据分析。在实际问题中,T检验可以帮助决策者快速、准确地评估不同组间的差异是否具有统计学意义,从而做出明智的决策。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2023-02-22 上传
2023-02-22 上传
2023-08-07 上传
2023-02-11 上传
2024-07-20 上传
2023-03-16 上传
仁义礼智信达
- 粉丝: 72
- 资源: 3
最新资源
- Java毕业设计项目:校园二手交易网站开发指南
- Blaseball Plus插件开发与构建教程
- Deno Express:模仿Node.js Express的Deno Web服务器解决方案
- coc-snippets: 强化coc.nvim代码片段体验
- Java面向对象编程语言特性解析与学生信息管理系统开发
- 掌握Java实现硬盘链接技术:LinkDisks深度解析
- 基于Springboot和Vue的Java网盘系统开发
- jMonkeyEngine3 SDK:Netbeans集成的3D应用开发利器
- Python家庭作业指南与实践技巧
- Java企业级Web项目实践指南
- Eureka注册中心与Go客户端使用指南
- TsinghuaNet客户端:跨平台校园网联网解决方案
- 掌握lazycsv:C++中高效解析CSV文件的单头库
- FSDAF遥感影像时空融合python实现教程
- Envato Markets分析工具扩展:监控销售与评论
- Kotlin实现NumPy绑定:提升数组数据处理性能