修正MOEA/D算法在多目标最优电力流动问题中的应用

"修正的MOEA / D方法解决多目标最优潮流问题" 本文是一篇研究论文，探讨了修正的多目标进化算法分解（Modified Multi-Objective Evolutionary Algorithm based on Decomposition, MOEA/D）方法在解决多目标最优潮流（Multi-objective Optimal Power Flow, MOPF）问题中的应用。最优潮流问题是电力系统优化的关键组成部分，旨在确定在满足一系列约束条件下，如何高效、经济地分配和传输电力。 传统的单目标最优潮流问题主要关注最小化发电成本，但现代电力系统中，多目标优化变得越来越重要，包括最小化燃料成本、降低污染排放、保障电网稳定性等多个相互竞争的目标。因此，MOPF问题需要同时考虑这些目标并找到一个平衡点，即所谓的帕累托最优解集。 MOEA/D是一种基于分解的多目标优化算法，其基本思想是将复杂的问题分解成多个子问题，然后通过独立优化这些子问题来寻找多目标问题的全局解决方案。在本研究中，作者对原始的MOEA/D进行了改进，以更好地适应MOPF问题的特性。这种修正可能涉及改进适应度函数、调整种群分布策略或优化决策变量的处理方式，以提高算法的收敛速度和解的质量。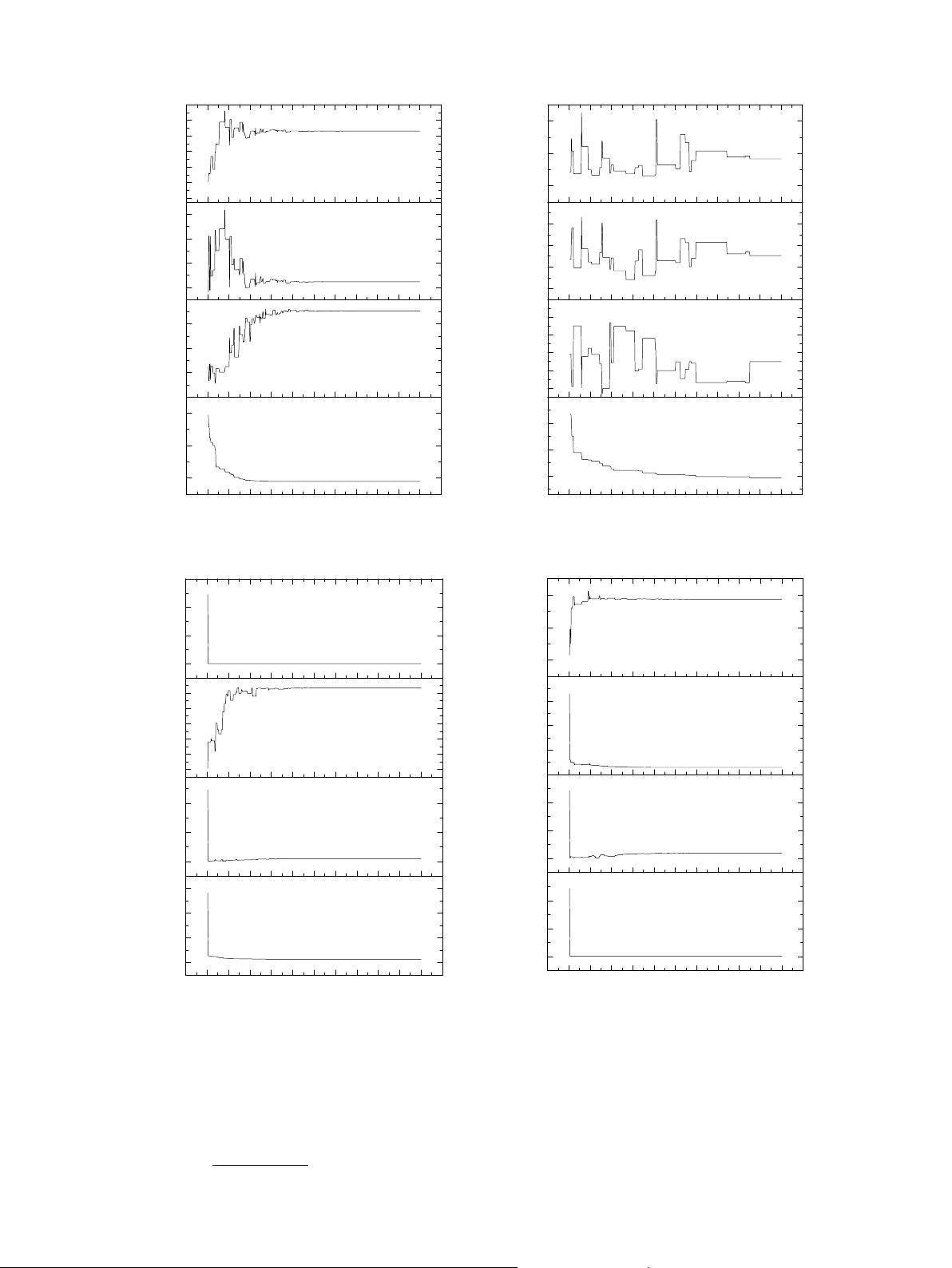 此外，文中还可能对比了修正后的MOEA/D与其他流行的多目标优化算法，如多目标粒子群优化（MOPSO）和非支配排序遗传算法第二代（NSGA-II）。这些比较旨在验证新方法的有效性和优势。通过模拟实验和性能指标分析，研究可能展示了修正的MOEA/D在解决MOPF问题时的优越性能，例如更好的帕累托前沿覆盖率和均匀性。 关键词涵盖了多目标优化、最优潮流问题、MOEA/D、MOPSO和NSGA-II，这些都是电力系统优化和计算进化算法领域的核心概念。该研究对于理解如何利用高级优化技术处理复杂的电力系统问题具有重要意义，并为未来的研究提供了新的视角和方法。