朴素贝叶斯算法详解：从原理到应用

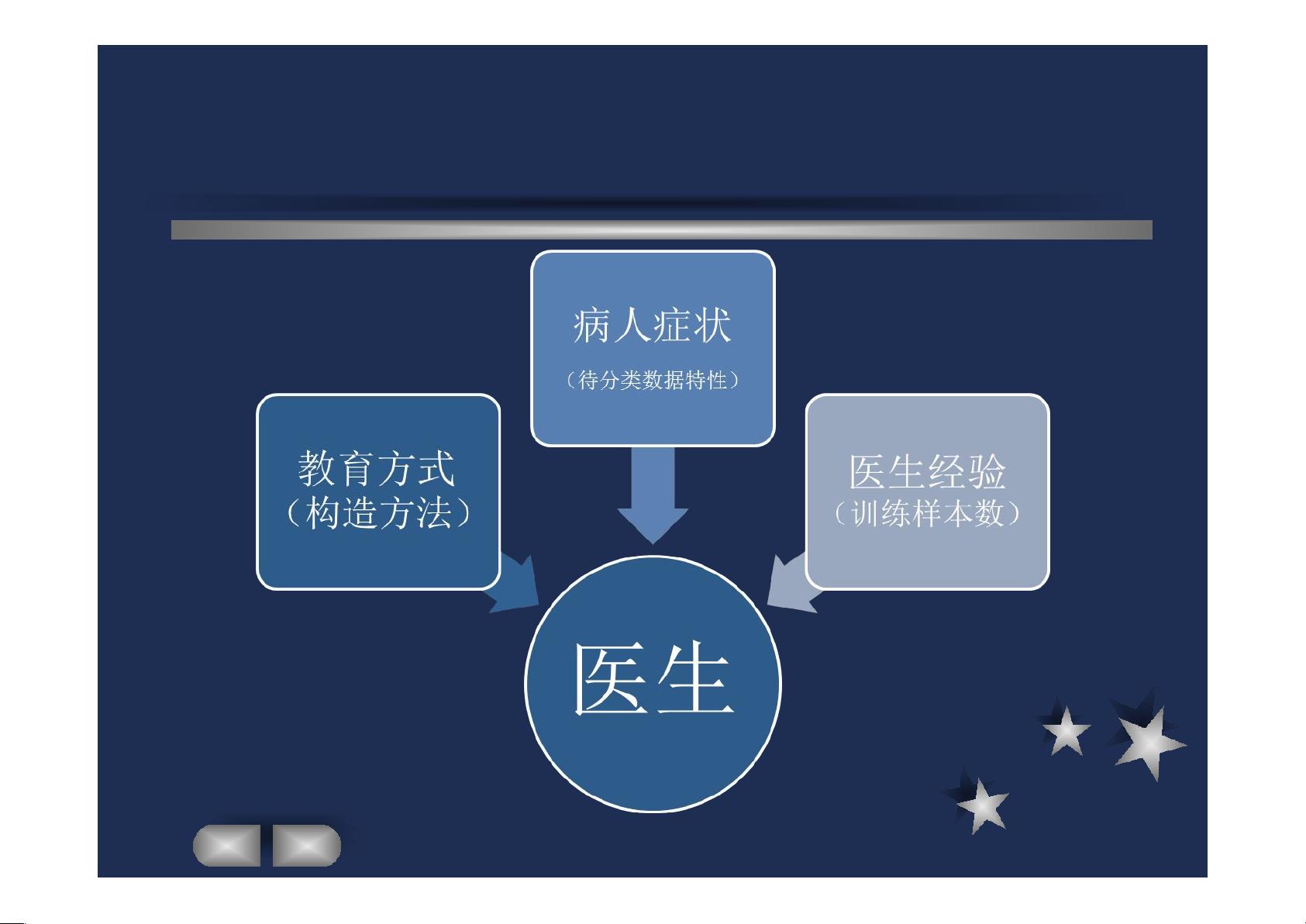
"大数据十大经典算法Navie_Bayes讲解PPT" 朴素贝叶斯算法是大数据分析领域中的一个重要算法，尤其在文本分类、垃圾邮件过滤、推荐系统等场景中广泛应用。它基于概率论中的贝叶斯定理，通过计算先验概率和条件概率来进行预测。本资料主要讲解了朴素贝叶斯算法的基本原理、处理流程以及一个实际的购买电脑的案例。 朴素贝叶斯算法的核心思想是贝叶斯定理，它描述了在已知某些证据的情况下，一个假设的概率如何根据先验概率进行更新。在分类问题中，我们试图找到一个类别，使得给定输入特征的情况下，该类别的后验概率最大。 算法分为三个阶段： 1. 准备阶段：首先，需要选择具有代表性的特征属性，并对这些属性进行适当的划分。然后，通过人工或自动方式选取一部分数据作为训练样本，以构建分类模型。 2. 分类器训练阶段：在这个阶段，计算每个类别在训练数据中出现的频率，以及每个特征属性对每个类别的条件概率。条件概率是指在某一类别下，某个特征取特定值的概率。例如，在购买电脑的例子中，会计算购买电脑的人群中，年龄小于等于30岁的概率，收入中等的概率，是学生与否的概率，以及信用评级较低的概率。 3. 应用阶段：利用训练好的分类器对新的、未标记的数据进行分类。通过计算待分类项在每个类别的后验概率，选择后验概率最大的类别作为预测结果。 在购买电脑实例中，朴素贝叶斯算法会计算年龄、收入、是否是学生和信用评级这四个特征对于是否购买电脑的条件概率。例如，计算在购买电脑的人群中，年龄小于等于30岁的概率，以及不购买电脑人群中这个概率，以此类推。这些概率将用于决定新用户是否可能购买电脑。 朴素贝叶斯算法的“朴素”一词来源于它的假设：各个特征之间相互独立。这意味着每个特征对分类结果的影响是独立的，不考虑特征之间的关联性。这种假设简化了计算，但可能在某些复杂数据集上导致性能下降。然而，即使在特征之间存在某种程度的相关性时，朴素贝叶斯算法仍能表现出相当不错的性能，特别是在数据量大且特征之间相关性不强的情况下。 朴素贝叶斯算法因其简单、高效和易于理解而被广泛采用。尽管它的假设可能过于简化，但在许多实际问题中，它仍然能够提供准确的分类结果。通过理解和掌握朴素贝叶斯算法，数据分析师和机器学习工程师可以更好地解决各种分类问题，尤其是在资源有限或需要快速响应的环境中。