分治法在大整数乘法中的应用与效率分析

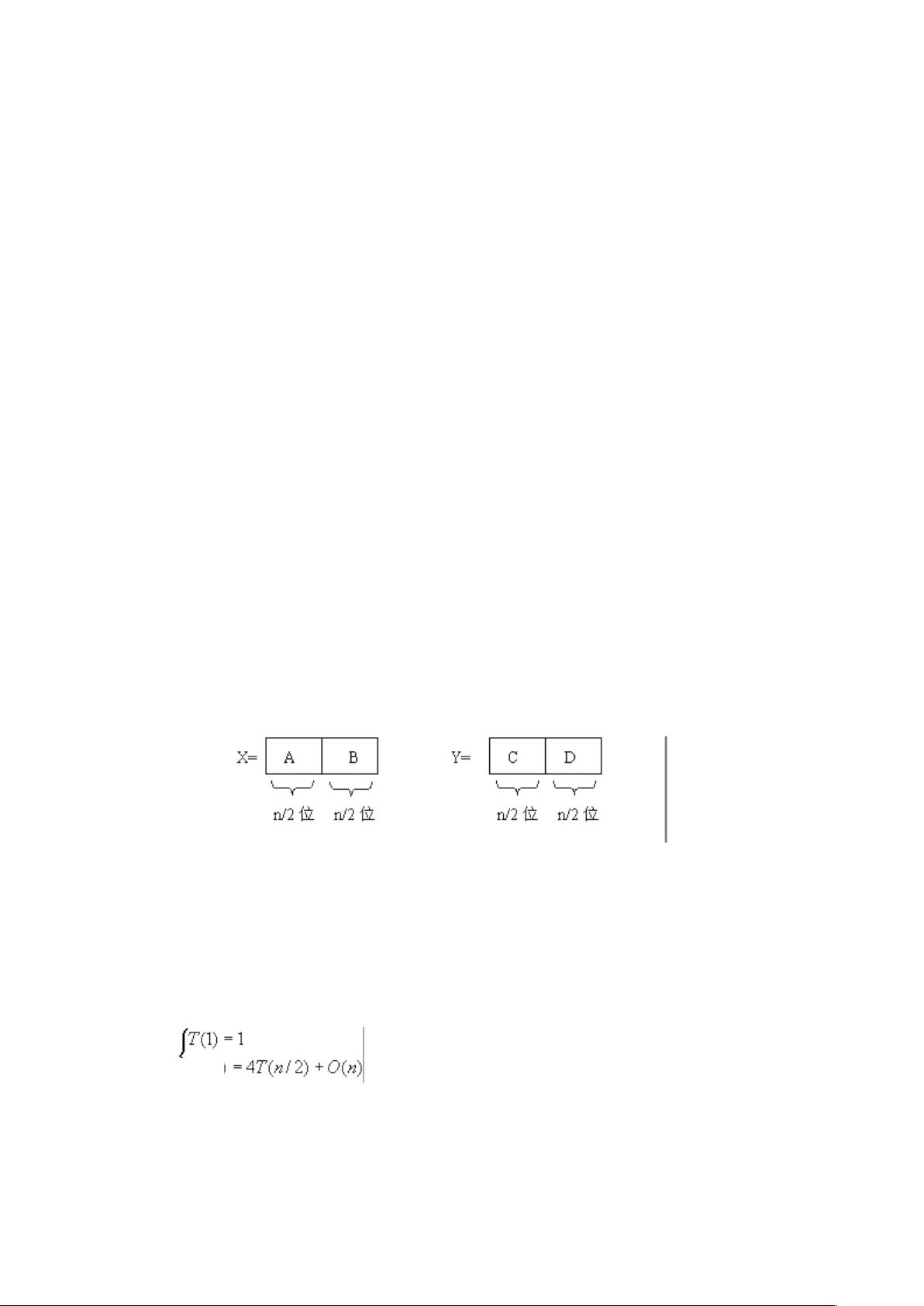
"该资源是一份关于计算机算法设计与分析的复习资料，涵盖了分治法的概念和典型实例，特别讨论了大整数乘法的两种实现方式：小学手算方法和分治法，并对这两种方法进行了效率分析。" 在计算机科学中，算法设计和分析是核心部分，它涉及解决问题的有效策略和计算复杂性的评估。分治法是一种常用的算法设计策略，其基本思想是将大问题分解为小问题，然后分别解决这些小问题，最后将结果合并，以求解原问题。分治法的典型流程通常包括三个步骤：分解、解决子问题和合并结果。在给定的资料中，分治法被应用到大整数乘法问题上。 大整数乘法是一个典型的计算密集型问题，尤其在处理大规模数据时。资源中对比了两种不同的计算方法：一是基于小学手算方法的程序实现，二是采用分治法的设计。 1. 小学手算方法：这是一种直观的乘法方法，但效率较低。对于两个n位的十进制整数X和Y，需要进行O(n^2)步运算（每个1位数的乘法或加法视为一步）。因此，其时间复杂度为O(n^2)，这种方法在处理大量数据时显得效率低下。 2. 分治法实现：为了提高效率，可以使用分治法将大整数乘法转化为多个较小规模的乘法和加法操作。将X和Y各分为两段，每段n/2位，然后根据乘法的分配律重新表示乘积，从而减少乘法次数。具体来说，大整数乘法可以通过4次n/2位整数的乘法和3次不超过2n位的整数加法完成，加上2次移位操作，总共需要O(n)步。然而，这种算法的时间复杂度仍然是O(n^2)，因为每个n/2位的乘法仍需要O(n^2)步。 为了进一步优化，可以继续探索其他算法，例如Karatsuba乘法或Toom–Cook算法，它们通过更高级的分解和重组策略，可以显著减少乘法的数量，从而降低计算复杂性。例如，Karatsuba乘法在最坏情况下的时间复杂度为O(n^1.585)，优于原始的分治法。 该复习资料深入浅出地介绍了分治法的原理，并通过大整数乘法这一实例展示了如何运用分治法设计算法。同时，资料也揭示了算法设计中优化的重要性，即通过改变问题的表示和处理方式，可以大大提高算法的效率。这对于学习和理解算法设计与分析具有很高的价值。