Matlab编程实战：矩阵运算、逆矩阵、特征值分解与多项式处理

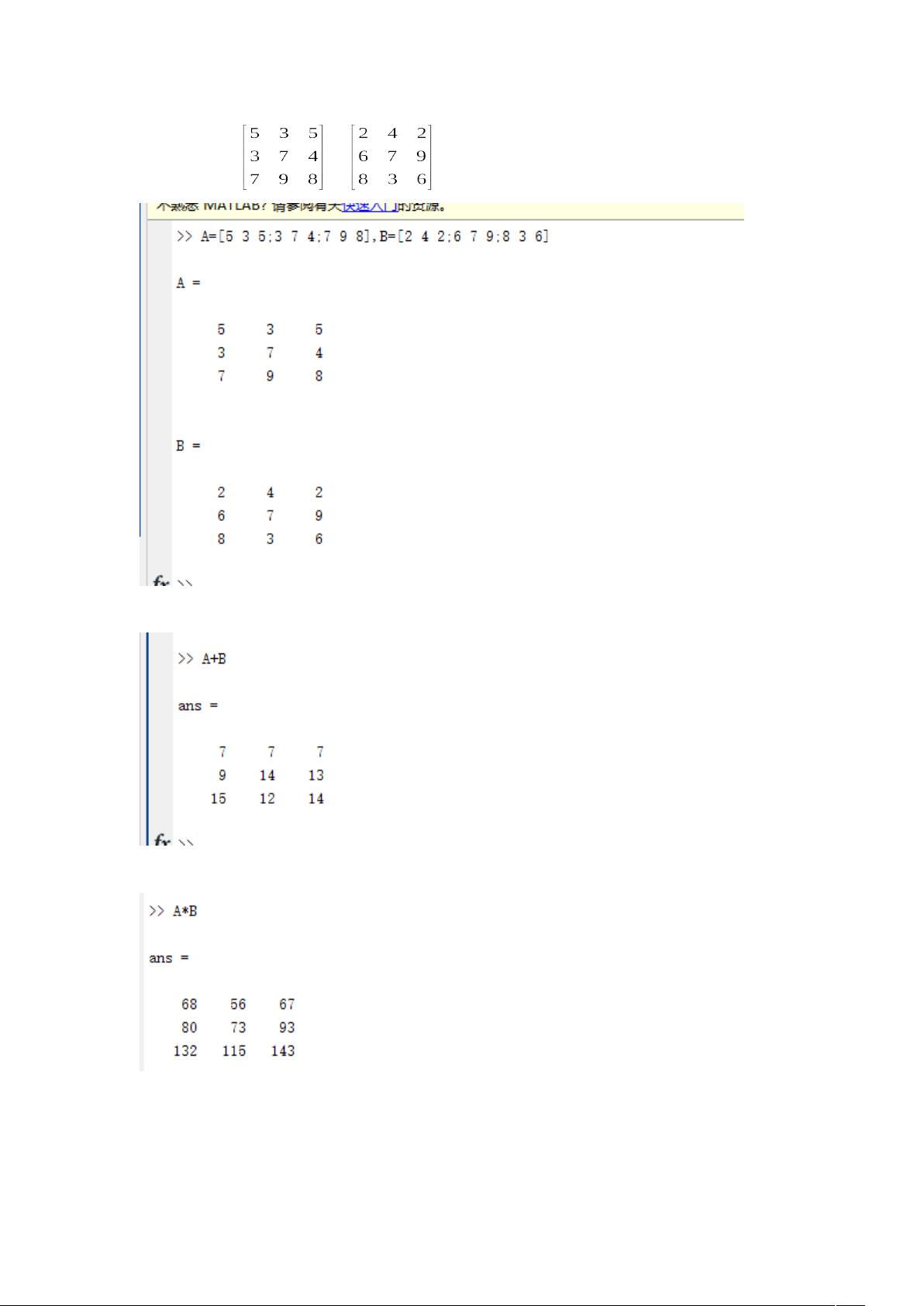
本资源是一份针对MATLAB编程的习题集，涵盖了矩阵运算、线性代数、向量和矩阵的生成、统计分析、多项式操作以及信号处理等多个方面的知识点。让我们逐一解析： 1. 矩阵运算：题目涉及矩阵的加法、乘法和特殊运算，如各元素的乘积以及Kronecker积。Kronecker积是两个矩阵的逐元素相乘，结果是一个更大的矩阵。例如，对于矩阵A和B，Kronecker积[A,B]的计算结果展示了矩阵乘法的复杂扩展。 2. 线性代数问题：要求解一个线性方程组，首先计算矩阵A的逆矩阵C，然后通过C与向量B的乘积得到X，这是求解线性系统的基本步骤，对于数值计算和数据分析具有实际应用价值。 3. 特征值分解：对矩阵进行特征值分解可以揭示矩阵的内在结构，包括特征值（表示特征向量的标量因子）和特征向量（反映矩阵在不同方向的行为）。这个过程在数值分析和机器学习中常用。 4. 对角矩阵生成：通过给定的复数向量，创建一个对角矩阵，这有助于理解和处理复数向量和矩阵的操作，尤其是在信号处理和控制系统中。 5. 随机向量生成与卷积：生成具有特定均值和方差的高斯向量，并利用均匀分布生成另一个向量，然后进行卷积操作，这涉及到随机数生成和信号处理中的基本概念。 6. 多项式求解：求解三次多项式的根，这对于数值方法、数学建模和计算机图形学中的函数拟合非常关键。 7. 多项式乘法：多项式乘法展示了MATLAB在处理代数表达式的能力，特别是在科学计算和工程设计中的应用。 8. 部分分式展开：这是一个复杂数学运算，用于简化多项式表达式，常用于控制系统设计和信号处理中的滤波器设计。 9. 微积分应用：计算正弦函数y=sin(x)在指定区间内的最大值、最小值、均值和标准差，这体现了MATLAB在数值积分和数据分析中的功能。 这份MATLAB习题集涵盖了基础的矩阵操作、线性代数、概率统计、代数函数以及数值分析等多个核心领域，旨在帮助学习者提升MATLAB编程技能并理解其实用性。通过解决这些习题，学生可以深化对MATLAB的理解，并将其应用于实际问题的求解中。