二维泊松方程非等间距有限差分数值解法

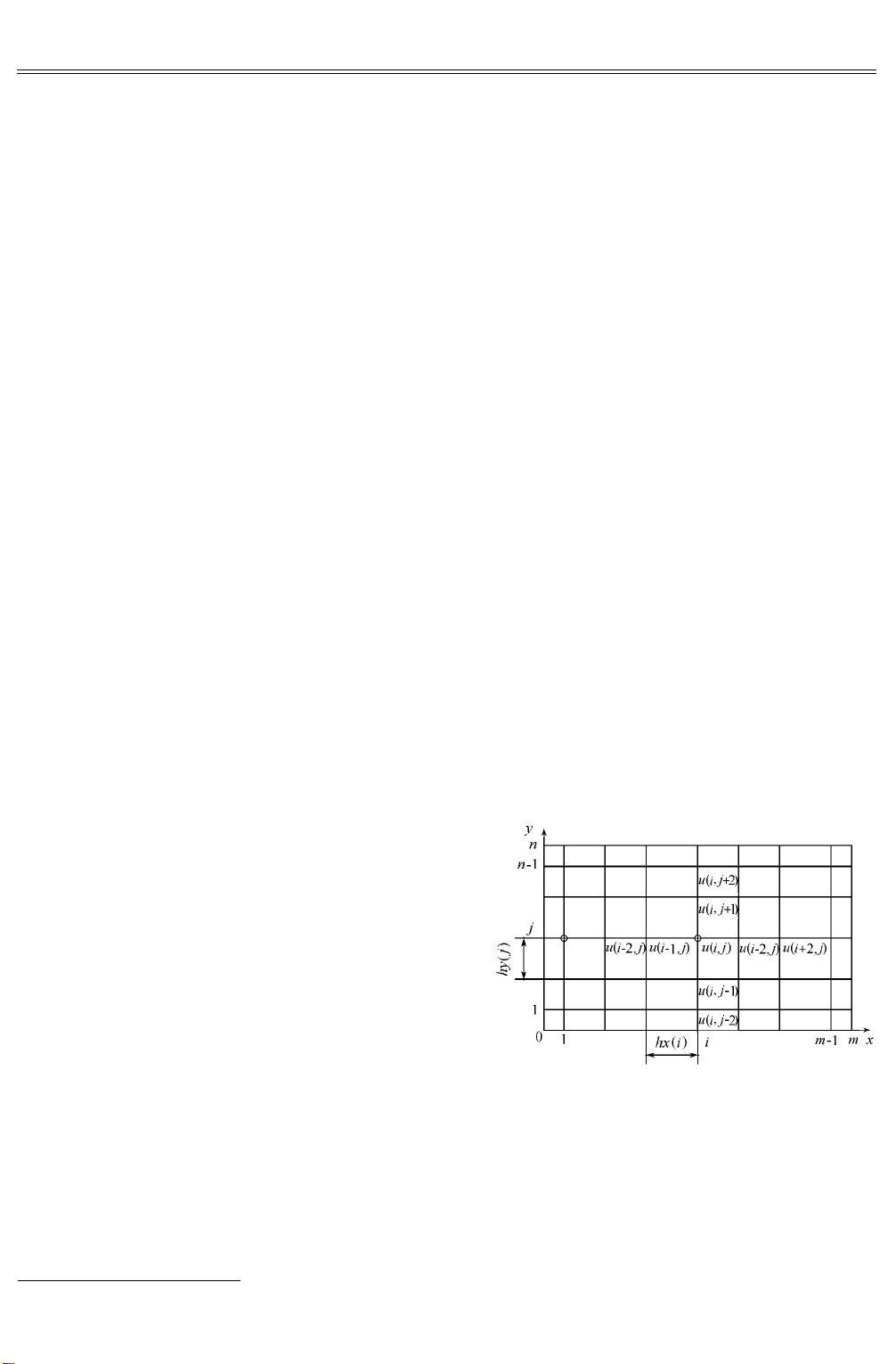
"泊松方程非等间距有限差分的数值求解方法 (2006年) - 采用3阶精度中心差分格式对Dirichlet边界条件下的二维泊松方程进行离散，近边界网格点处采用2阶精度差分格式，利用超松弛迭代进行矩阵求解。" 泊松方程是数学和物理领域中的一种基本偏微分方程，广泛应用于流体动力学、渗流理论、电磁学、传热学和结构力学等多个学科。在实际问题中，由于泊松方程解析解的稀少性，对其求解通常依赖于数值方法。本文探讨了一种适用于非等间距网格的泊松方程数值求解方法，该方法结合了高阶精度的差分格式和迭代求解技术。 曹卫东、陆昌根和钱建华提出的方案采用了3阶精度的中心差分格式来离散在Dirichlet边界条件下的二维泊松方程。在靠近边界的网格点处，他们则采用了2阶精度的差分格式，以处理边界条件的影响。这种方法的优点在于能够适应非均匀网格，同时保持较高的计算精度。在数值求解过程中，他们运用了超松弛迭代法，这是一种常用的迭代方法，能够快速地求解线性系统的大型稀疏矩阵，具有良好的收敛性能。 传统的等间距网格方法，如5点或9点中心差分，虽然简单，但在网格间距较大时可能无法保证足够的精度。而9点紧致格式虽然可以提供更高的精度，但需要网格在特定方向上等间距，这在实际问题中可能难以满足。对于那些需要在局部精细网格化（如流体动力学中的边界层）的问题，非等间距网格方法显得尤为重要，因为它允许在需要的地方增加网格密度，同时在其他区域保持较稀疏的网格，从而节省计算资源。 文中提到的数值算例展示了这种方法的有效性，通过对比分析证明了非等间距网格下采用3阶精度中心差分和2阶精度边界差分格式结合超松弛迭代的数值解具有快速收敛和高精度的特性。这种方法不仅适用于泊松方程，还可以推广到其他类型的偏微分方程求解中。 此外，文章还提到了在流体力学和边界层理论中的应用，特别是在处理近壁面流动特性的计算时，非等间距网格的优势尤为明显。Gamet等人已经成功地将类似的方法应用于Navier-Stokes方程的数值计算，这进一步证实了这种方法的通用性和实用性。 这篇论文提供了非等间距网格下求解泊松方程的一个高效数值策略，对于需要精确解决复杂物理问题的科研和工程实践具有重要价值。通过这种方法，研究人员能够在保持计算效率的同时，获取更精确的解决方案，特别是在处理具有强烈空间变化特性的物理问题时。