SPSS假设检验：理解与应用

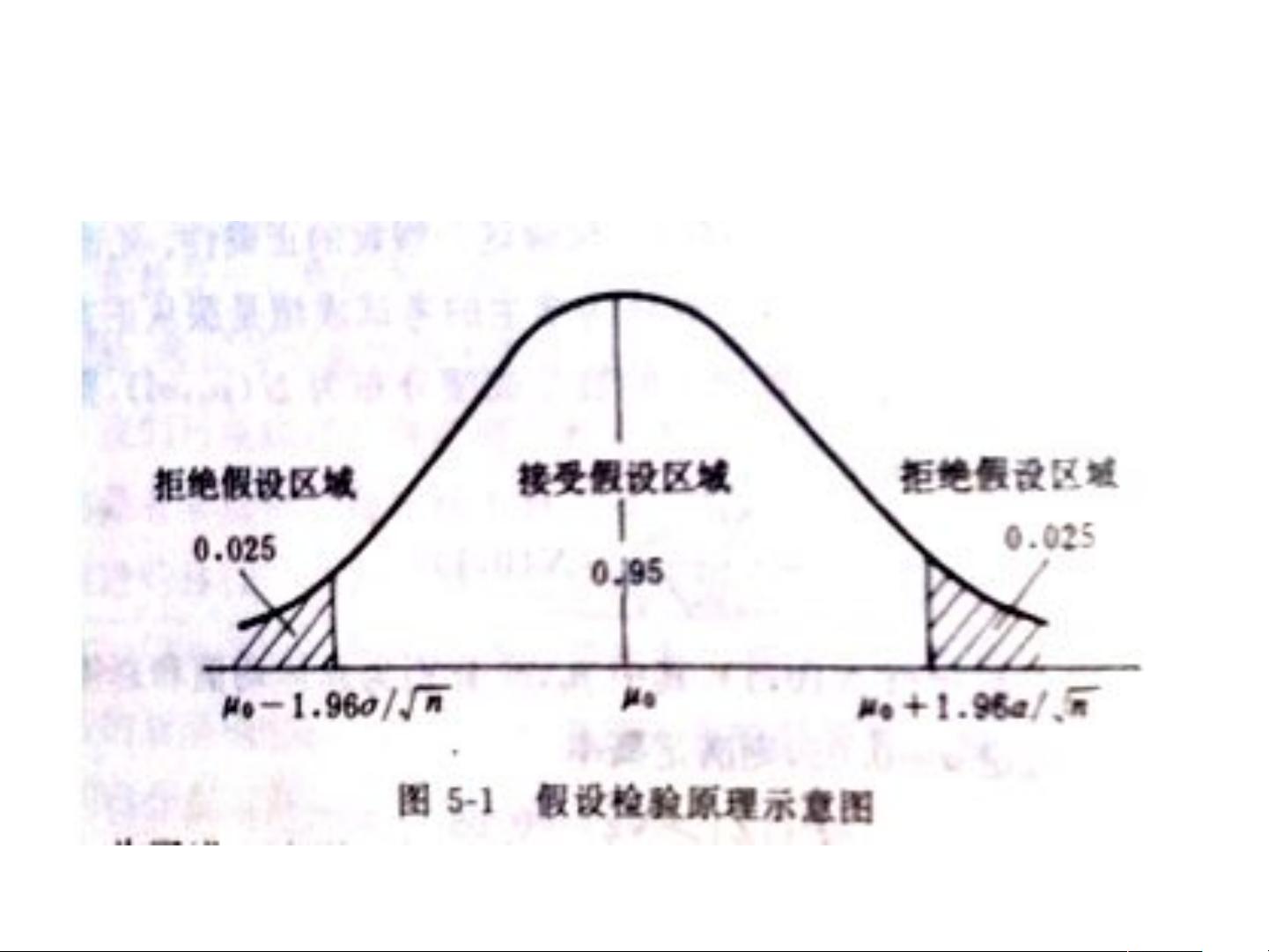
"spss假设检验" 在统计学中，假设检验是一种决定性工具，它帮助研究人员判断观察到的样本数据是否支持或反驳关于总体的一个特定假设。SPSS（Statistical Product and Service Solutions）作为一个强大的统计分析软件，提供了丰富的假设检验功能，使得用户可以轻松处理各种类型的假设测试。在本摘要中，我们将深入探讨SPSS中的假设检验，特别是针对两正态总体均值差异和方差差数的显著性检验。 首先，假设检验的基本问题是基于小概率原理，即认为极小概率事件在一次实验中几乎不会发生。如果一个事件的发生概率非常低，比如小于5%，那么在实际观测到这个事件时，我们倾向于否定原来的假设，转而接受备择假设。例如，在产品质量检查中，如果一个被认为99%合格率的产品批次出现不合格品，我们会质疑其真实合格率。 在SPSS中，假设检验通常涉及两个假设：原假设（H0）和备择假设（H1）。原假设通常是默认的零假设，即没有显著差异或者效果，而备择假设则提出存在某种差异或效果。当数据支持备择假设时，我们拒绝原假设。这两个假设是互斥的，每个假设检验只能在这两者之间进行选择。 8.1.3 假设检验的检验统计量是衡量数据与原假设之间偏离程度的关键指标。例如，t检验和z检验是用于判断两个正态总体均值差异的统计量，它们取决于样本的均值、标准差以及样本大小。如果总体方差未知，通常使用t检验；如果已知，使用z检验。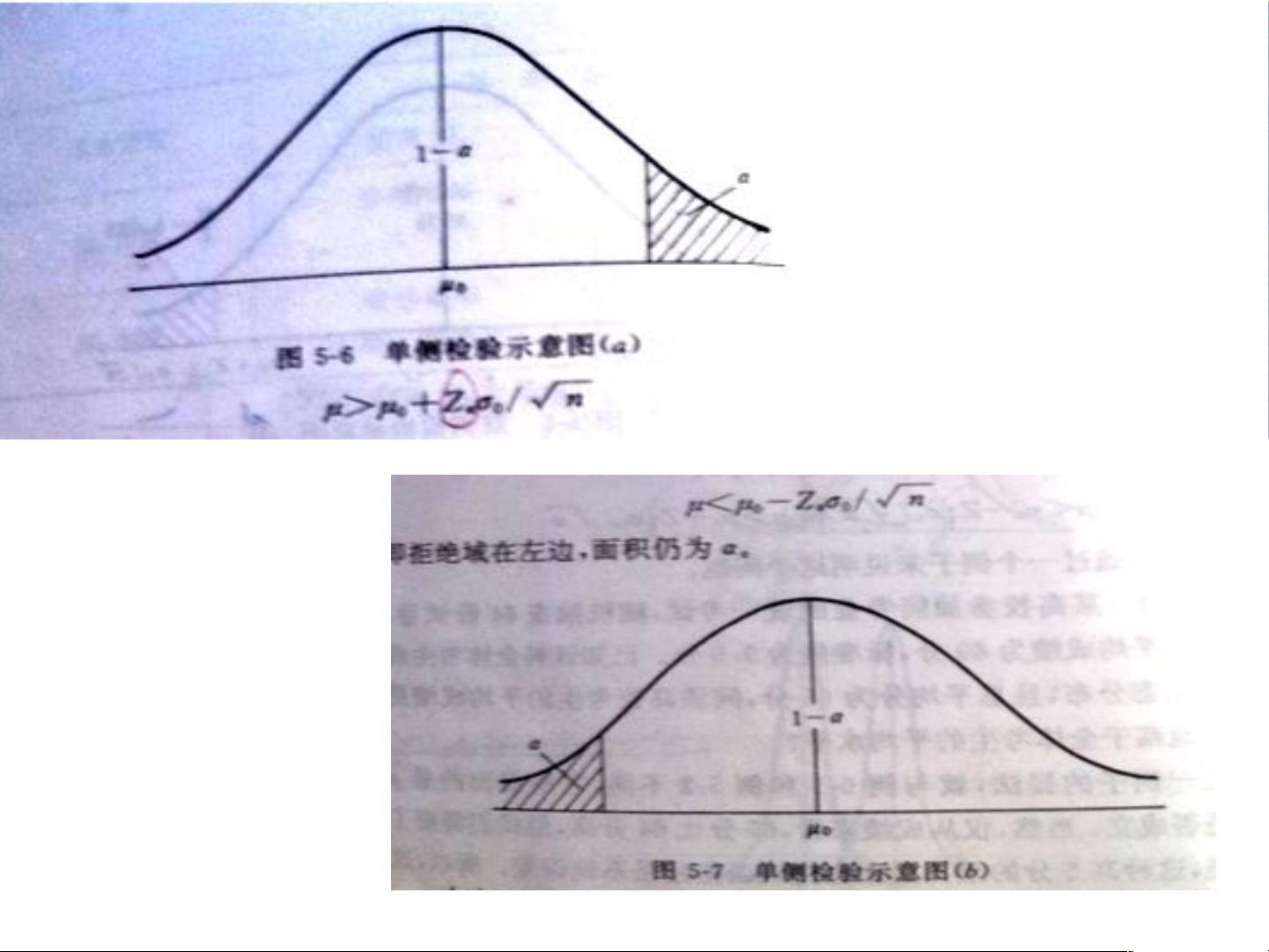 8.1.4 显著性水平（通常设置为0.05）定义了我们愿意接受的犯错误的风险程度。当p值（检验统计量对应的概率）小于显著性水平时，我们说结果是显著的，并拒绝原假设。例如，在上述教学法案例中，我们需要计算新旧教学法下数学成绩的平均值差异的p值，如果p值小于0.05，我们就可以说新教学法的效果显著不同于旧方法。 8.2 总体平均数的显著性检验，如单样本t检验，用于比较样本均值与已知总体均值的差异。例如，研究某种药物治疗效果时，可以将治疗组的平均改善值与预期改善值进行比较。 8.3 双总体平均数差异的显著性检验，如独立样本t检验，用于比较两个独立样本的均值是否存在显著差异。在教育研究中，可能用它来评估不同教学方法对学生成绩的影响。 在SPSS中，这些检验可以通过相应的菜单选项执行，用户只需输入数据，选择合适的检验类型，软件将自动计算统计量，提供p值和决策结果。同时，SPSS还支持其他类型的假设检验，如方差分析（ANOVA）、卡方检验、相关性分析等，涵盖了广泛的应用场景。 SPSS的假设检验功能为科研工作者提供了有力的工具，无论是在自然科学、技术科学还是社会科学领域，都能有效分析数据，确定变量间的显著关系，从而得出科学结论。通过理解并熟练运用这些假设检验方法，用户可以更好地利用SPSS进行数据分析和决策。