密码学基础：对称与公钥体制，安全挑战与应用

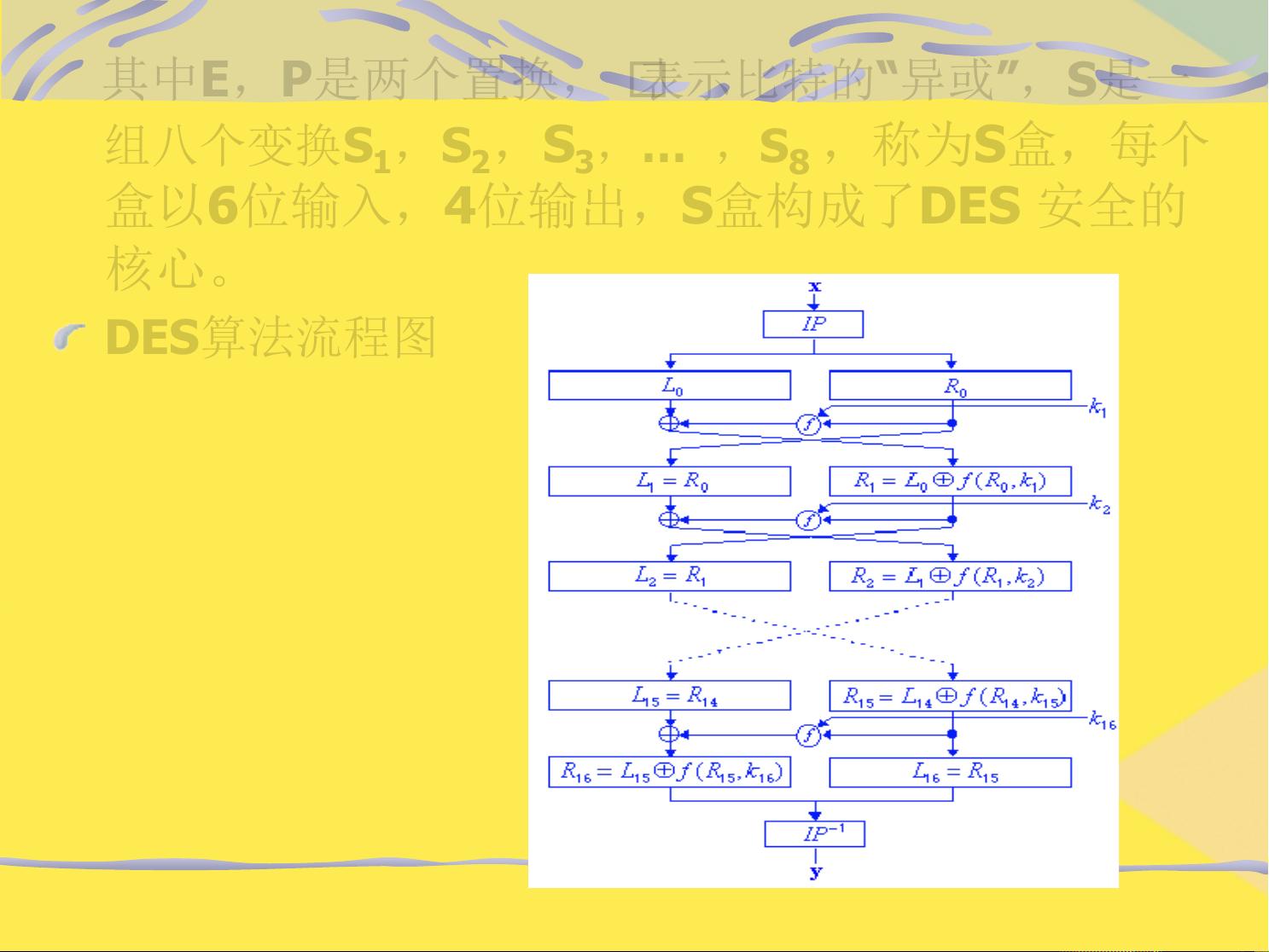
本章节主要讨论的是计算机信息安全原理与技术中的密码学基础，涵盖了对称密码体制和公钥密码体制的核心概念，以及相关的加密和解密方法。在密码学的早期，古典密码如单表置换密码（如凯撒密码）、多表置换密码（如维吉尼亚密码）被用于保密通信。随着科技的发展，近代密码如DES（数据加密标准）和Diffie-Hellman公钥体制的引入，极大地提升了信息安全水平。 第2章详细阐述了密码学的基本概念，包括现代密码系统的构成要素，如明文空间M、密文空间C、密钥空间K、加密算法E和解密算法D，这些构成了一个完整的密码体制。在对称密码体制中，加密和解密使用同一把密钥，例如RSA算法中，通过计算两个大素数的乘积n，其安全性基于n的素因子分解难以实现。 此外，该章节还介绍了散列函数，它们常用于数据完整性检查和数字签名，确保信息的不可变性和真实性。数字签名是一种利用公钥密码体制实现的技术，签名者用私钥加密数据，接收者用公钥验证，确保只有签名者能创建有效签名。信息隐藏和数字水印技术也是密码学的应用之一，它们可以保护信息不被未经授权的修改或复制。 在信息攻击方面，区分了主动攻击（如恶意篡改、删除数据）、被动攻击（如截取、窃取信息）和无意攻击（如操作失误）。密码学的目标是防范这些攻击，保护数据的保密性、真实性、完整性。 对于公钥密码体制，如RSA，其中加密密钥b是公开的，而解密密钥a（即私钥）必须保持机密。为了保证安全，关键在于如何保密计算上不可行的解密过程，即寻找满足一定条件的逆元a，这就涉及到欧拉函数φ(n)和素因子分解。 本章内容深入浅出地介绍了密码学的基石，展示了其在保障信息安全中的核心作用，无论是对称还是非对称加密技术，都是现代信息技术体系中不可或缺的一部分。