VHDL实现16阶Kaiser窗低通FIR滤波器

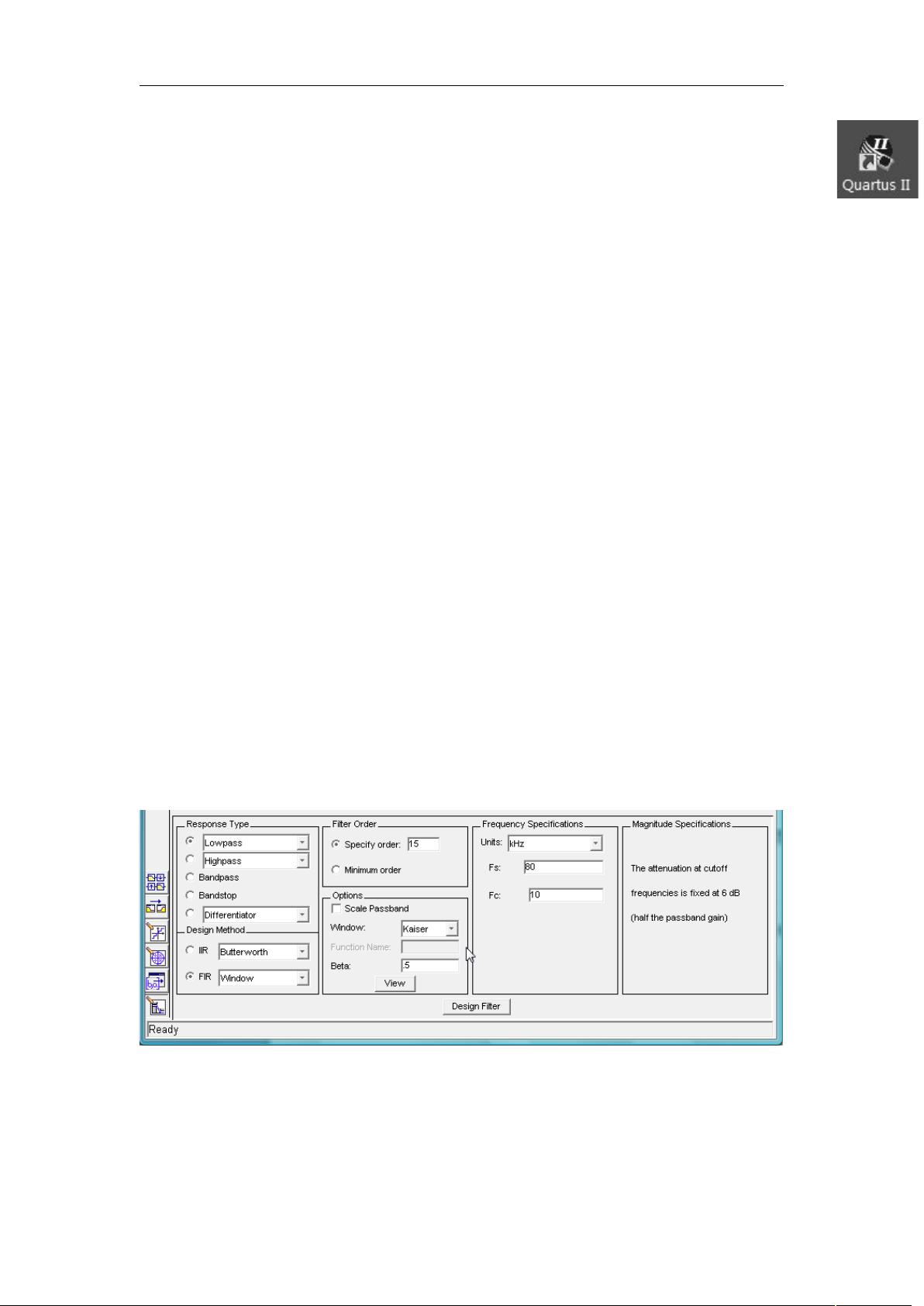
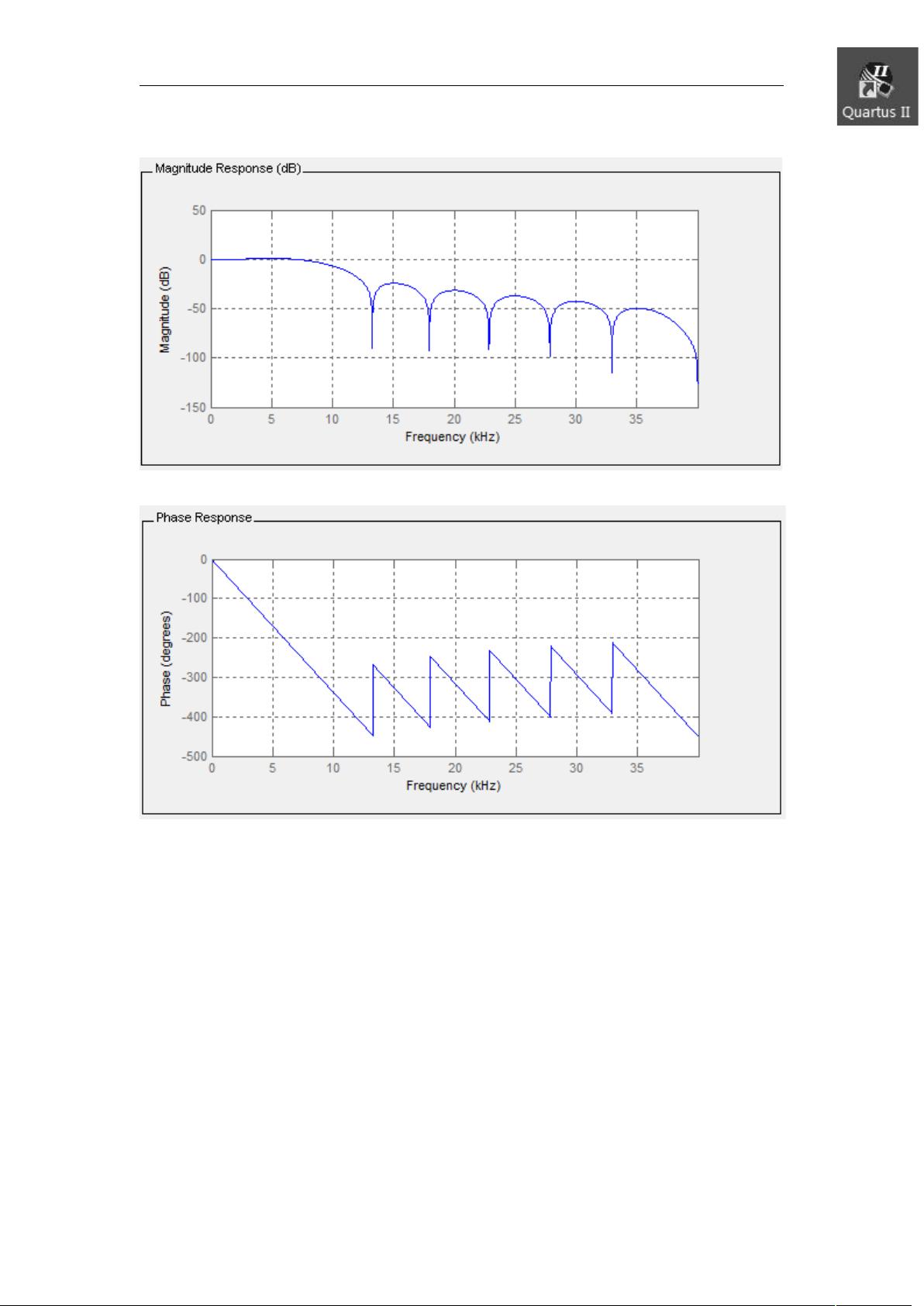
"本文主要介绍了如何使用VHDL来实现16阶的低通线性相位FIR滤波器，该滤波器应用于带通滤波，具有特定的采样频率和截止频率。设计中采用了Kaiser窗函数，输入和输出序列均为10位有符号数。" 在数字信号处理领域，FIR（Finite Impulse Response）滤波器是一种广泛应用的滤波器类型。它们因为其稳定性、可实现性和线性相位特性而备受青睐。在VHDL中实现FIR滤波器，可以利用硬件描述语言的优势，将滤波算法转化为可综合的逻辑电路，从而在 FPGA 或 ASIC 上高效执行。 在本设计中，滤波器的目标是实现一个16阶的低通滤波效果，用于带通滤波。采样频率Fs设定为80KHz，而截止频率Fc设定为10KHz。设计使用了Kaiser窗函数方法，这是一种优化滤波器系数的方法，可以提供更好的频率选择性和滚降特性。Kaiser窗函数的参数Beta设置为0.5，影响了滤波器的过渡带宽度和阻带衰减。 FIR滤波器的线性相位特性意味着其输出信号与输入信号的相位关系是线性的，不引入非线性相位失真。这种特性在要求信号传输无明显相位扭曲的应用中非常重要，比如数据通信和图像处理。线性相位FIR滤波器的结构可以通过适当的时间延迟调整，使其在保持线性相位的同时，适应不同的系统需求。 在VHDL实现中，FIR滤波器通常采用直接型结构，即通过级联乘法器和加法器来计算输出序列。对于一个M阶的滤波器，需要M个系数，每个系数对应一个乘法器，然后通过(M-1)个加法器将结果相加。在本例中，16阶滤波器需要16个乘法器和15个加法器。线性相位的特性使得滤波器的系数呈现对称或反对称，这减少了乘法器的数量，对于对称结构的滤波器，乘法器数量可以减半。 设计过程通常包括以下步骤：首先在MATLAB等工具中计算出满足设计指标的滤波器系数；然后，使用VHDL编写滤波器的结构，包括定义滤波器的输入、输出以及系数寄存器；最后，通过综合工具将VHDL代码转化为硬件逻辑，并在目标平台上进行仿真和验证。 在VHDL代码中，滤波器的核心部分通常是一个循环结构，该结构迭代计算每个输出样本。每一迭代会涉及乘法器和加法器的操作，这些操作对应于FIR滤波器的冲激响应系数。滤波器的系数存储在 ROM（只读存储器）中，以确保在运行时能快速访问。 VHDL实现的FIR滤波器是一个高效、灵活的解决方案，尤其适用于实时信号处理。通过精确计算滤波器系数和精心设计的硬件结构，可以在满足设计指标的同时，达到最优的性能和资源利用率。