C++函数嵌套与自定义函数探索：求最大公约数

本文将深入探讨C++中的函数嵌套以及如何使用自定义函数来解决实际问题，例如通过求最大公约数来解决特定的算法挑战。 在C++编程中，函数是一段可重用的代码块，它执行特定的任务并可能返回结果。函数定义通常包括返回类型、函数名和参数列表，如下面的`zc`函数所示，用于计算三角形的周长： ```cpp int zc(int a, int b, int c) { return a + b + c; } ``` 函数调用是通过在其名称后面放置括号并传递所需的参数来完成的。例如，在`main`函数中调用`zc`函数： ```cpp int main() { int c = zc(3, 8, 6); // 调用zc函数 cout << c << endl; return 0; } ``` 函数可以分为有返回值和无返回值两种类型。有返回值的函数（如`zc`）必须包含`return`语句来提供函数执行的结果。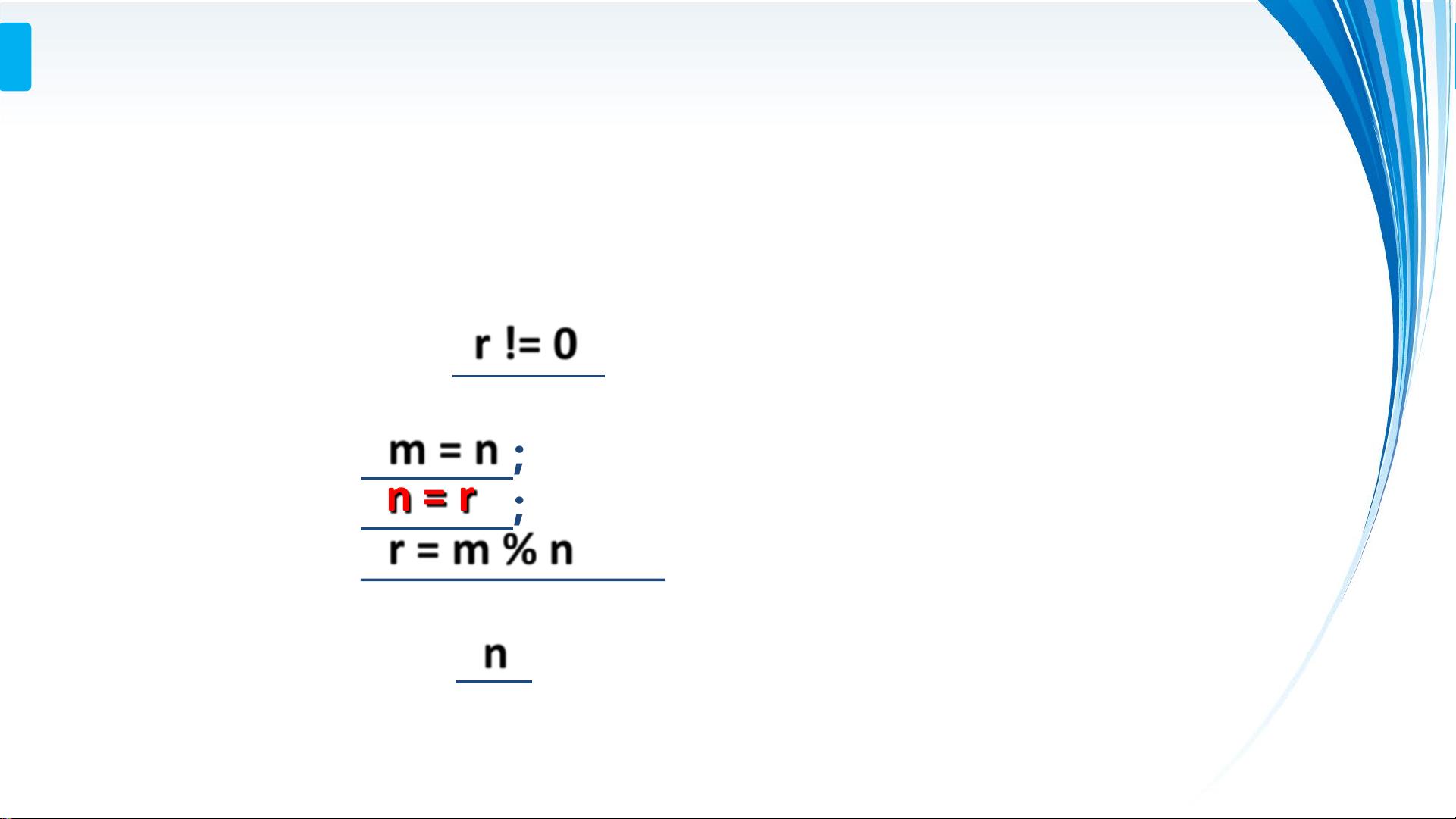而无返回值的函数，如`void print(int n)`，其返回语句可以省略，因为它们不返回任何值： ```cpp void print(int n) { for (int i = 1; i <= n; ++i) { cout << i << endl; } } ``` 现在，我们转向一个具体的算法问题：给定一组长度不同的钢材，需要找出一种切割方案，使得所有小段的长度相同，并且切割次数最少。这实际上是一个求最大公约数（Greatest Common Divisor, GCD）的问题。对于N个整数，我们可以采用欧几里得算法（Euclidean Algorithm）来高效地找到它们的最大公约数。假设我们有数组`numbers[]`包含N个整数，可以使用以下函数来计算它们的最大公约数： ```cpp int findGCD(int numbers[], int N) { int result = numbers[0]; for (int i = 1; i < N; i++) { result = __gcd(result, numbers[i]); } return result; } // 使用内置的__gcd函数，它是求两个数最大公约数的C++库函数 int __gcd(int a, int b) { if (b == 0) return a; return __gcd(b, a % b); } ``` 然后，对于输入样例`4 422812`，调用`findGCD`函数，输出将是钢材小段的长度： ```cpp int main() { int N; cin >> N; int numbers[N]; for (int i = 0; i < N; i++) { cin >> numbers[i]; } int gcd = findGCD(numbers, N); cout << gcd << endl; return 0; } ``` 总结来说，C++的函数嵌套和自定义函数是程序设计中的重要工具，它们允许我们将复杂的问题分解为可管理的模块。在这个案例中，我们利用了自定义函数来解决一个实际的算法问题，即求解一组整数的最大公约数，从而确定钢材的最优切割长度。通过这种方式，我们能够更好地理解C++的函数机制及其在解决实际问题中的应用。