"MATLAB模糊控制仿真实例分析与建模技术"
78 浏览量
更新于2024-01-31
2
收藏 2.03MB PPT 举报
本文将详细介绍使用MATLAB的模糊逻辑工具箱进行仿真的实例分析。MATLAB的模糊逻辑工具箱是在Matlab4.2以后的版本中推出的,为仿真模糊控制系统提供了很大的方便。
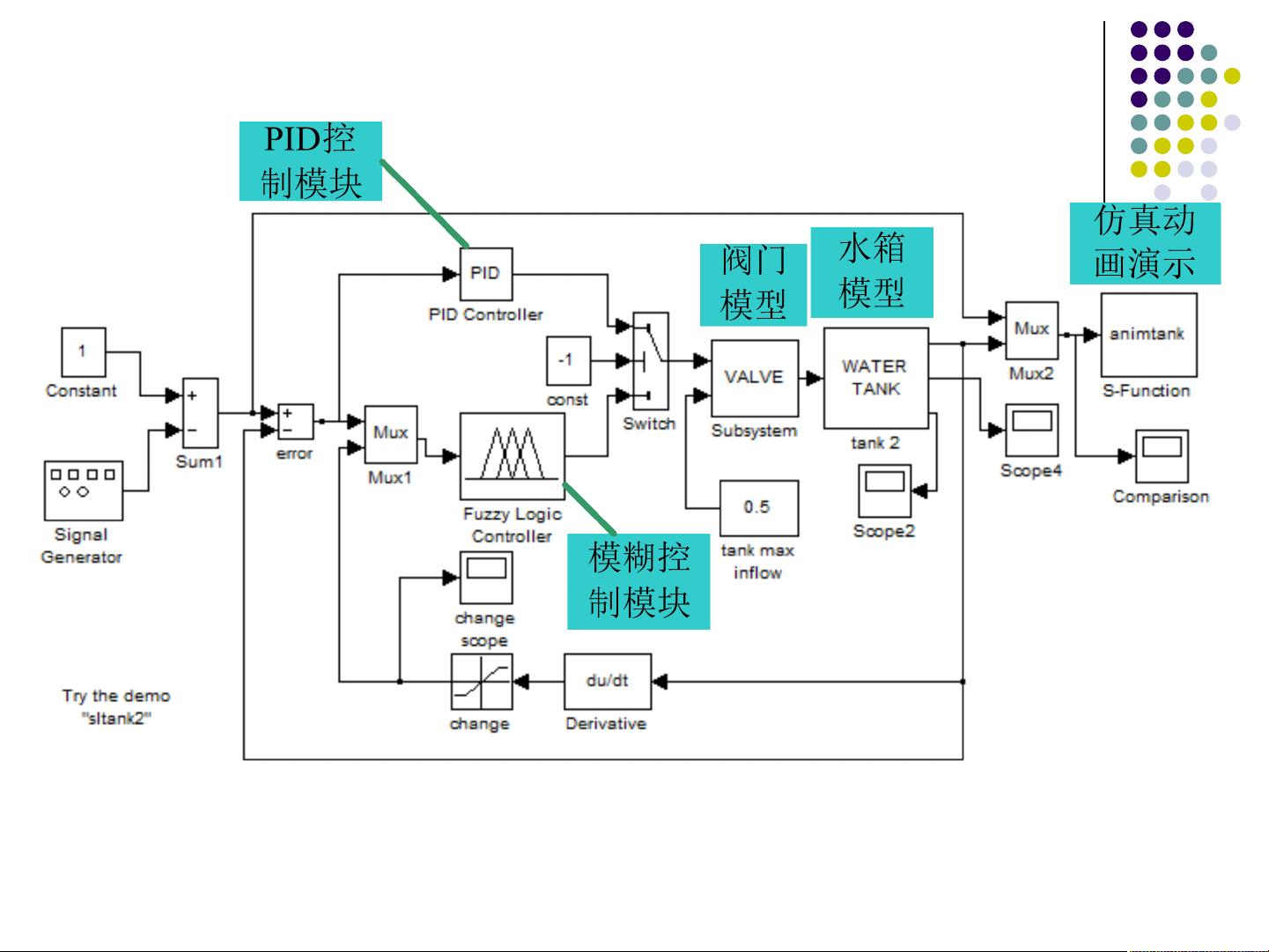
在Simulink环境下对PID控制系统进行建模是非常方便的,而模糊控制系统与PID控制系统的结构基本相同,仅仅是控制器不同。因此,使用Matlab的模糊逻辑工具箱对模糊控制系统进行建模也非常方便。
对模糊控制系统的建模关键是对模糊控制器的建模。Matlab软件提供了一个模糊推理系统(FIS)编辑器,只要在Matlab命令窗口键入Fuzzy就可以进入模糊控制器编辑环境。该编辑器可以设计和显示模糊推理系统的一些基本信息,如推理系统的名称,输入、输出变量的个数与名称,模糊推理系统的类型、解模糊方法等。其中模糊推理系统可以采用Mandani或Sugeuo两种类型,解模糊方法有最大隶属度法、重心法、加权平均等。
在MATLAB中打开模糊推理系统编辑器很简单。只需要在MATLAB的命令窗口内输入“fuzzy”命令即可打开该编辑器。通过该编辑器,可以方便地定义输入变量和输出变量的模糊集合,设定模糊推理规则,并选择相应的模糊控制器类型和解模糊方法。通过这些设定,可以方便地对模糊控制系统进行建模和仿真。
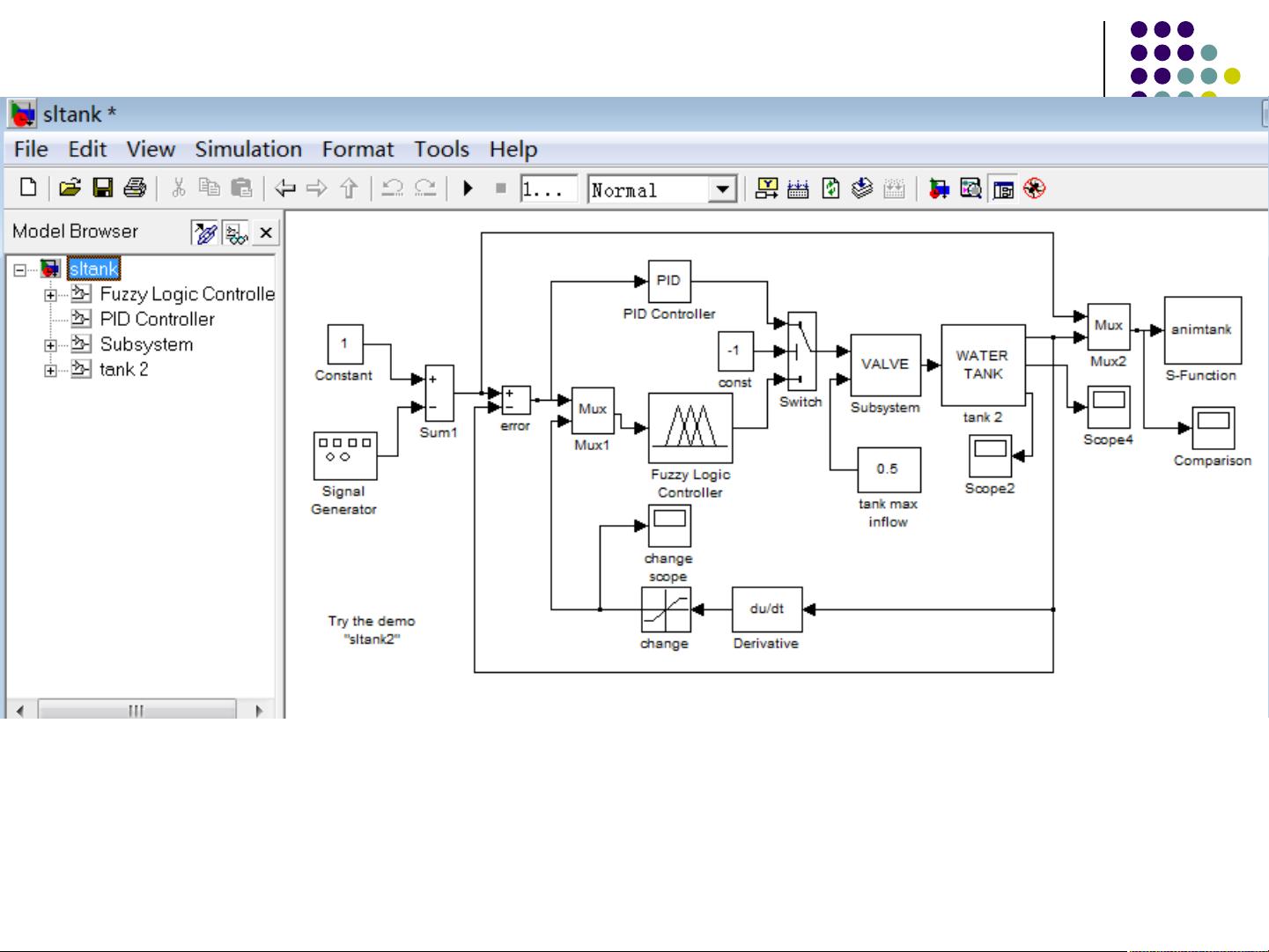
为了验证模糊控制系统的性能,需要进行仿真实验。在MATLAB中,可以使用Simulink环境对模糊控制系统进行仿真。在Simulink中,可以方便地将模糊控制系统与被控对象进行连接,构建出完整的模糊控制系统模型。然后,可以设定输入信号和初始条件,进行仿真实验,并分析仿真结果,评估模糊控制系统的性能。
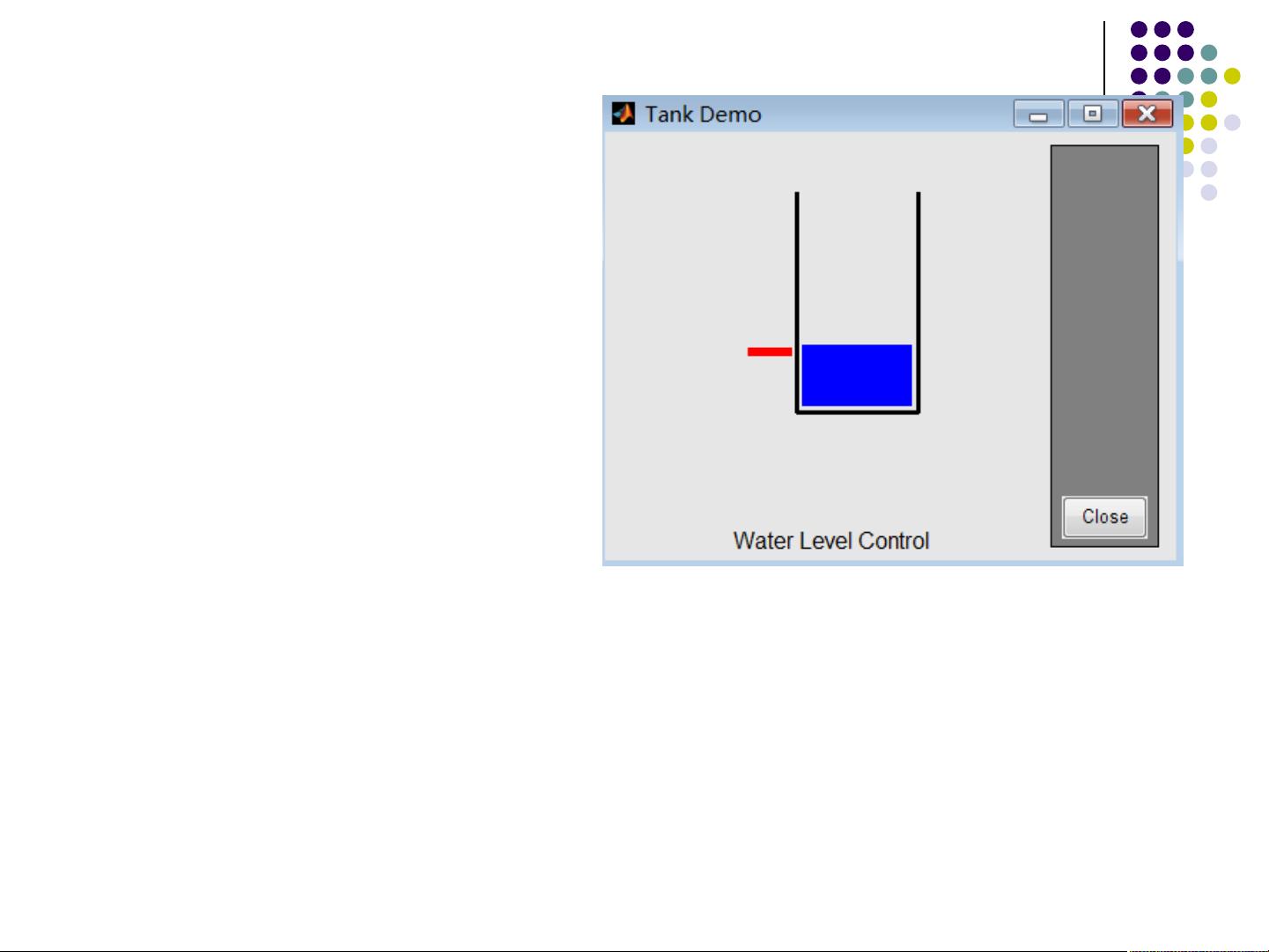
在模糊控制仿真实例分析中,我们可以选择一个具体的被控对象,如一个水箱水位控制系统。首先,在模糊推理系统编辑器中定义输入变量(如水箱水位的误差、误差的变化率)和输出变量(如水泵的控制信号),并设定相应的模糊集合和模糊推理规则。然后,通过Simulink环境,将模糊控制器与水箱水位系统进行连接,构建出完整的模糊控制系统模型。最后,设置输入信号和初始条件,进行仿真实验,并分析仿真结果。
通过以上的实例分析可知,使用MATLAB的模糊逻辑工具箱进行仿真实验非常方便。通过该工具箱,可以设计并构建出复杂的模糊控制系统模型,并进行仿真实验。这样可以方便地验证模糊控制系统的性能,并进行参数调整和优化。因此,MATLAB的模糊逻辑工具箱是模糊控制系统设计与仿真的重要工具,对于模糊控制技术的研究和应用具有很大的帮助。
586 浏览量
2021-10-10 上传
127 浏览量
147 浏览量
2021-10-07 上传
2023-07-29 上传
2023-07-04 上传
matlab大师
- 粉丝: 2838
最新资源
- InfoQ中文站:Struts2入门指南
- 探索函数式编程:Haskell语言实践
- 在Linux AS4上安装MySQL 5.0.27的详细步骤
- Linux环境下安装配置JDK1.5、Tomcat5.5、Eclipse3.2及MyEclipse5.1指南
- MapGIS 7.0:嵌入式GIS开发平台详解与关键技术
- MATLAB编程风格与最佳实践
- 自顶向下语法分析方法:LL(1)文法与确定性分析
- Tapestry实战指南:探索动态Web应用开发
- MyEclipse安装指南:JDK与Tomcat设置详解
- Adobe Flash Video Encoder 中文指南
- 测试环境搭建与管理:要求、备份与恢复
- C语言经典编程习题解析:从100例中学习
- 高质量C/C++编程规范与指南
- JSP驱动的个性化网上书店系统开发与实现
- MediaTek MTK入门教程:软件架构与开发流程解析
- 学习Python:第二版详细指南