COL 12(11), 113302(2014) CHINESE OPTICS LETTERS November 10, 2014
1671-7694/2014/113302(4) 113302-1 © 2014 Chinese Optics Letters
Acquiring multi-spectral images by digital still cameras
based on XYZLMS interim connection space
Xiandou Zhang (张显斗)
*
, Qiang Wang (王 强), Genfu Yang (杨根福),
and Mengmeng Wang (王萌萌)
School of Digital Media and Art Design, Hangzhou Dianzi University,
Hangzhou 310018, China
*
Corresponding author: xiandouzhang@126.com
Received June 24, 2014; accepted September 11, 2014; posted online October 24, 2014
A method based on the XYZLMS interim connection space is proposed to accurately acquire the multi-spectral
images by digital still cameras. The XYZLMS values are rstly predicted from RGB values by polynomial
model with local training samples and then spectral reectance is constructed from XYZLMS values by
pseudo-inverse method. An experiment is implemented for multi-spectral image acquisition based on a
commercial digital still camera. The results indicate that multi-spectral images can be accurately acquired
except the very dark colors.
OCIS codes: 330.1715, 330.1730, 110.4234.
doi: 10.3788/COL201412.113302.
Multi-spectral images have great application prospects
in digital arching, computer vision, computer graphics,
high-delity color representation, and reproduction
[1–3]
.
There are many techniques for multi-spectral image
acquisition, such as multi-sensor based, lter based,
and light-emitting diode (LED) light sources-based
multi-spectral imaging systems
[4]
. Although they can
accurately obtain multi-spectral images, most of these
systems are complicated, expensive, and inconvenient,
which prevent many practical applications, such as
those in common illuminating environments with cam-
eras to get multi-spectral images
[5]
. Many methods have
been proposed to predict the spectral reectance from
RGB values of digital cameras, such as the widely used
Wiener method
[6,7]
and the constrained least-squares
(CLS) method
[8]
. In this work, a method based on com-
mon digital still cameras is proposed to acquire multi-
spectral images, and an experiment is implemented to
verify the performance of the proposed method.
The greatest diiculty for common cameras to acquire
multi-spectral images is that there are only three chan-
nels in the cameras. It is generally believed that at least
six channels are required to accurately acquire multi-
spectral images
[9]
. The XYZLMS interim connection space
has been proposed to accurately represent multi-spectral
images
[10]
. If the XYZLMS values can be accurately pre-
dicted from RGB values, then multi-spectral images
can be accurately acquired from the common cameras.
The XYZ values can be accurately predicted from RGB
values with polynomial, back propagation (BP) neural
network, and look-up table (LUT) methods
[11]
. Then the
key point is that how to predict LMS values from RGB
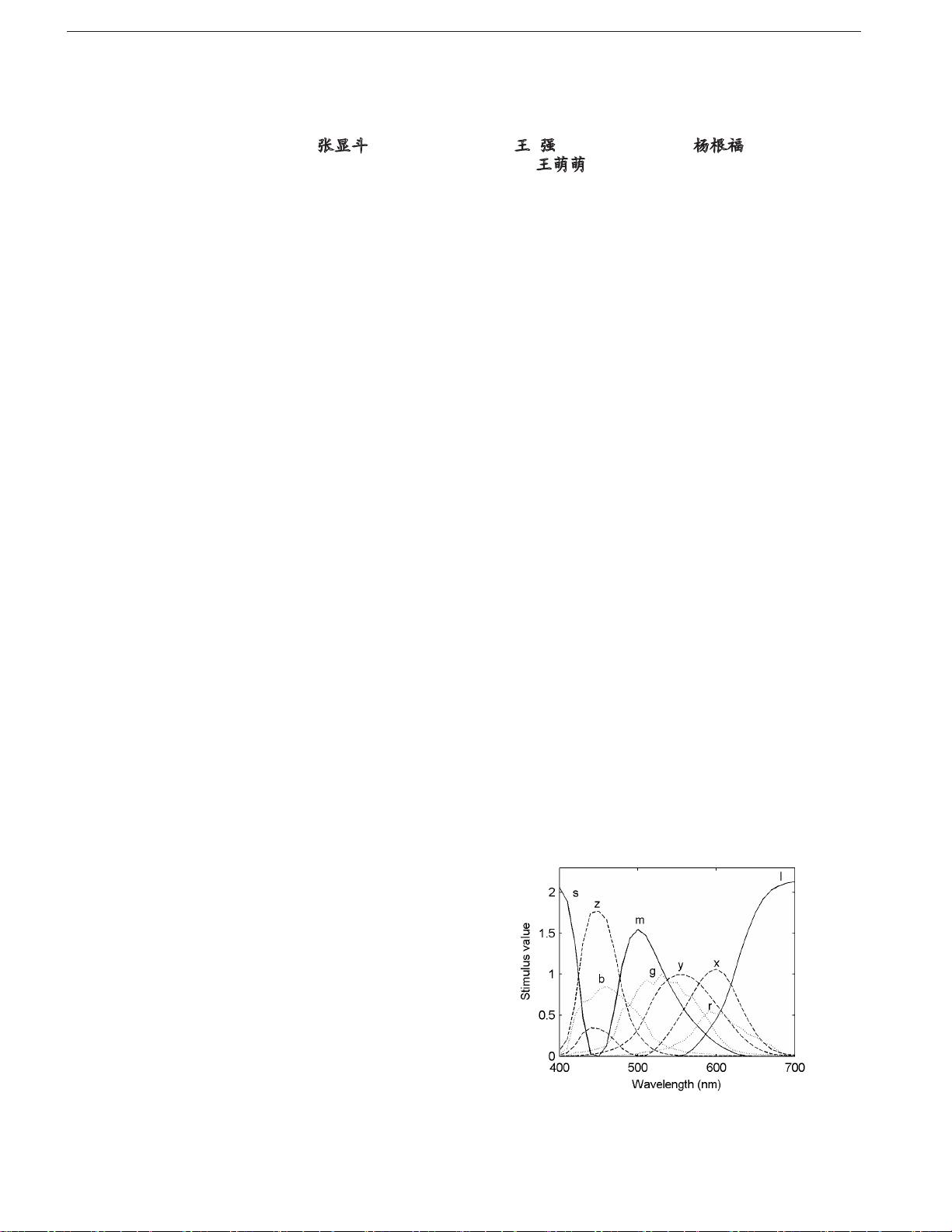
values. Figure 1 shows the x (λ), y (λ), z (λ), l (λ), m (λ),
and s (λ) stimulus values in the XYZLMS space, and
the spectral sensitivity functions r (λ), g (λ), and b (λ) of
a Cannon 60D commercial camera, which is measured
by a spectrophotometer
[12]
. It appears that the L and S
values cannot be accurately predicted as the correlation
relationship between l (λ), s (λ) and r (λ), g (λ), b (λ) is
low. Fortunately, the spectral reectances of real-world
objects are smooth functions of wavelength
[13]
. The L and
S values somehow have the same variation trend with
the RGB values, which can connect the correlation rela-
tionship between RGB and L, S values. In other words,
there are great possibilities for the prediction of L and S
values from RGB values for real-world objects. To verify
this point, an experiment was implemented for the Z
value prediction from RGB values, and similar conclu-
sion can be derived for the L and S values prediction.
As shown in Fig. 1, there is little correlation relationship
between z (λ) and r (λ), so both of the following polyno-
mial models were adopted for the Z value prediction to
investigate whether the R values have contribution to
the Z value prediction.
01 2 3 4 5 6
7 8 9 10
,
a rg a rb a gb a rgb
=++++ + +
++++
(1)
Fig. 1. Spectral distribution of the nine stimulus values.









