一元多项式相加相乘的链式存储实现

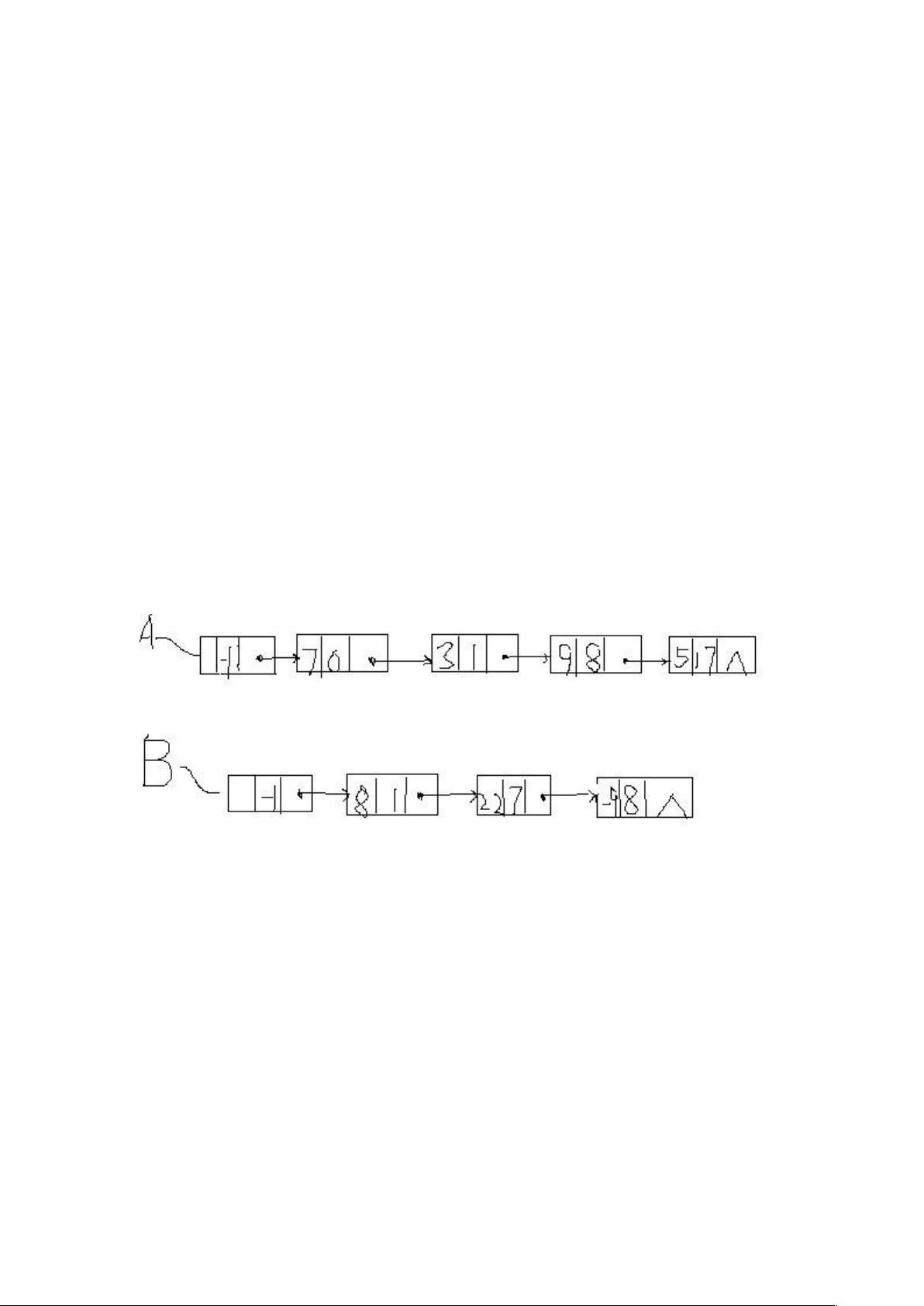
"数据结构课程设计，主要涉及一元多项式的加法和乘法运算，使用链式存储结构实现。" 在数据结构课程设计中，一个常见的任务是处理数学中的多项式运算，尤其是相加和相乘。本设计的重点是一元多项式的乘法，它在计算机科学中具有重要的应用，例如在符号计算、图像处理和信号处理等领域。一元多项式是由常数、变量及其幂次组成的数学表达式，如A(x) = 7 + 3x + 9x^8 + 5x^17和B(x) = 8x + 22x^7 - 9x^8。 为了高效地实现多项式的加法和乘法，通常采用链式存储结构，这是因为链表可以灵活地处理不同大小的多项式，避免了数组固定大小带来的限制。链表的每个节点包含系数（coef）和指数（expn）两个字段，以及指向下一个节点的指针。 对于一元多项式的加法，算法遵循以下规则： 1. 比较两个多项式中对应指数的项，如果指数相同，则将系数相加。如果和不为零，这个新的项将被添加到“和多项式”中。 2. 如果两个多项式中没有相同指数的项，那么这两个项都应当被保留到“和多项式”中。 在实现过程中，通过指针qa和qb分别遍历两个多项式链表，比较它们的指数项。有三种可能的情况： 1. 当qa所指节点的指数小于qb的指数，qa所指节点被添加到“和多项式”。 2. 如果qa的指数大于qb的指数，qb所指节点被添加。 3. 如果两者指数相等，将系数相加。若和为零，删除对应的节点；否则，更新qa所指节点的系数并释放qb所指节点。 一元多项式的乘法则更为复杂，因为它涉及到每个项与其他所有项的乘积。通常，乘法可以通过分配律将一个多项式中的每一项与另一个多项式中的每一项相乘，然后将结果合并。在链式存储结构中，这通常涉及创建一个新的链表来存储乘法的结果，每个节点表示一个乘积项。 为了实现这些操作，需要定义多项式（Polynomial）的抽象数据类型，如所示的`typedef struct LNode`，并实现相关的函数，包括： 1. `CreatPolyn`：输入多项式的系数和指数，构建有序链表表示多项式。 2. `DestroyPolyn`：销毁给定的多项式链表。 3. `PrintPolyn`：输出多项式链表的内容。 此外，还需要实现多项式乘法的具体算法，这通常涉及多次调用加法操作来组合各个乘积项。在实际编程中，还需要考虑错误处理和优化，比如使用适当的数据结构（如平衡树）来加速查找相同指数的项，以及优化内存管理，减少不必要的节点创建和销毁。