机器学习：误差源于偏差与方差

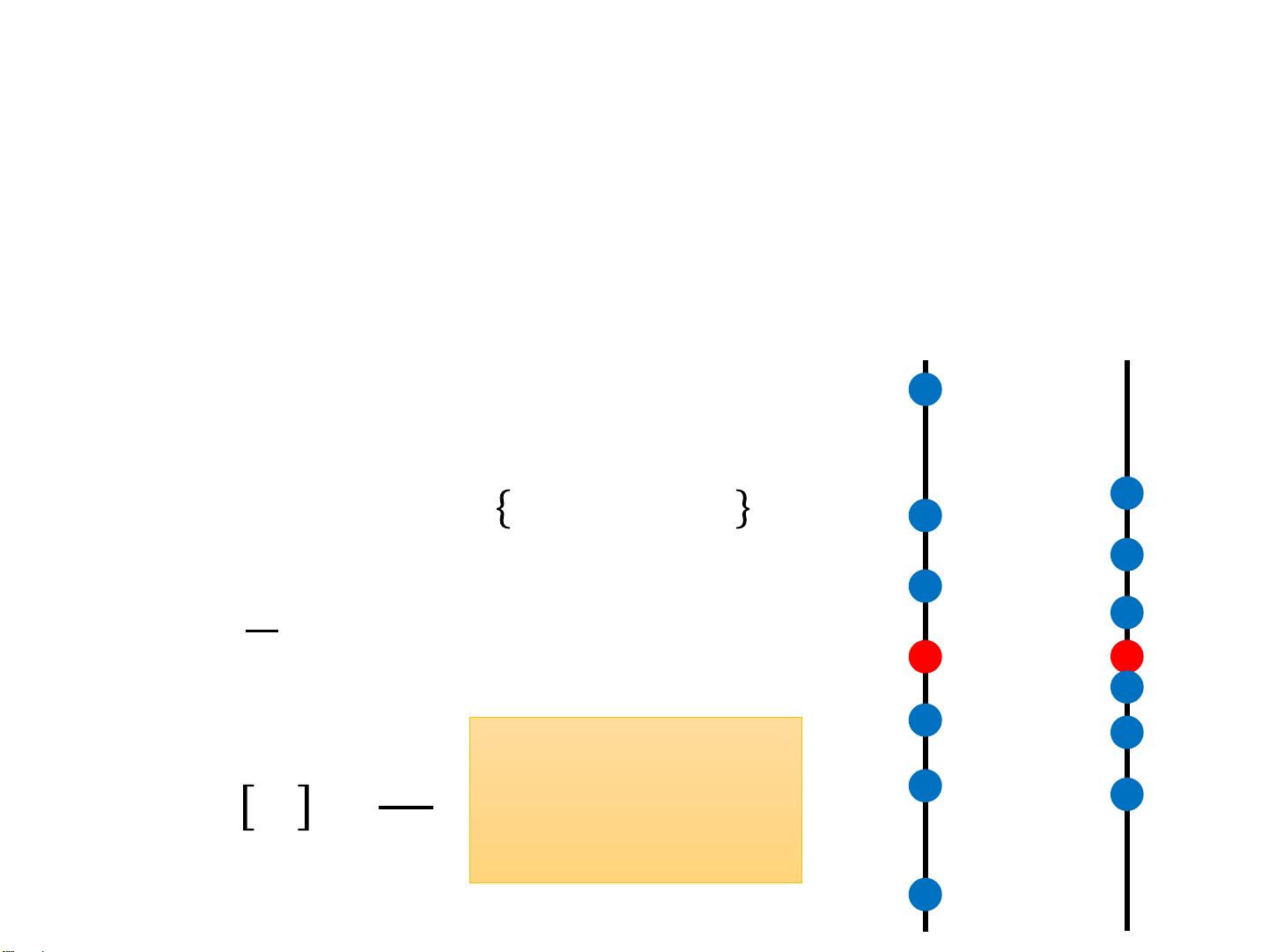
"这篇内容探讨了机器学习中的偏差（Bias）和方差（Variance）问题，以及它们在模型选择中的重要性。" 在机器学习领域，模型的性能不仅仅取决于模型的复杂度，而是由误差的两个主要成分——偏差和方差共同决定。偏差是指模型在试图学习数据时的固有误差，它衡量的是模型的预测能力与真实值之间的差距，即模型的期望预测与真实结果的平均差异。当模型过于简单，无法捕捉到数据集中的复杂模式时，就会出现高偏差，这通常导致模型欠拟合（Underfitting）。 方差则是指模型对训练数据中的噪声敏感程度，它描述了模型在训练数据集上的预测结果变化范围。如果一个模型的方差很高，那么即使在训练集上表现良好，它也可能在新的、未见过的数据上表现得很差，这是过拟合（Overfitting）的标志。模型复杂度过高往往会导致过拟合，因为模型会过度学习训练数据的细节，包括噪声。 以估计变量x的均值为例，我们假设均值为μ，方差为σ²。通过采样N个点x1, x2,..., xN，我们可以计算样本均值m作为μ的估计。当N足够大时，样本均值是一个无偏估计，即E[m] = μ。然而，样本均值的方差Var[m]依赖于样本数量N，较小的N会导致较大的方差，这意味着估计的稳定性较差。 对于变量x的方差估计，我们通常使用N-1除以N的修正项来减少偏差，如Bessel's correction。估计的方差Es = (N-1)/N * σ²。随着N的增加，这个估计会更接近真实的方差σ²，但当N较小时，该估计会偏向低估实际方差，此时的方差估计是有偏的。 模型选择的过程就是在这两者之间找到平衡，寻找偏差和方差的最佳折衷点。一个理想的模型应该有低偏差和低方差，但实际中，我们往往需要通过交叉验证、正则化等技术来调整模型复杂度，以降低过拟合或欠拟合的风险。例如，正则化通过引入惩罚项来限制模型参数的自由度，从而降低过拟合的可能性，同时保持模型的泛化能力。 理解和控制偏差与方差是优化机器学习模型性能的关键，它们是评估模型在新数据上的预测能力的重要指标。在实际应用中，我们需要不断地尝试不同的模型和参数，寻找那个能在训练数据和未知数据上都表现良好的平衡点。