July 10, 2007 / Vol. 5, No. 7 / CHINESE OPTICS LETTERS 393
Hyperspectral image compression using three-dimensional
significance tree splitting
Jing Huang (
ÿÿÿ
), Rihong Zhu (
ýýý
), Jianxin Li (
), and Yong He (
)
School of Electronic Engineering and Photoelectric Technology, Nanjing University of Science and Technology, Nanjing 210094
Received Nov ember 28, 2006
A three-dimensional (3D) wavelet coder based on 3D significance tree splitting is proposed for hyperspectral
image compression. 3D discrete wavelet transform (DWT) is applied to explore the spatial and spectral
correlations. Then the 3D significance tree structure is constructed in 3D wavelet domain, and wavelet
coefficients are encoded via 3D significance tree splitting. This proposed algorithm does not need to use
ordered lists, moreover it has less complexity and requires lower fixed memory than 3D set partitioning
in hierarchical trees (SPIHT) algorithm and 3 D set partitioned embedded block (SPECK) algorithm. The
numerical experiments on AVIRIS images show that the proposed algorithm outperforms 3D SPECK, and
has a minor loss of performance compared with 3D SPIHT. This algorithm is suitable for simple hardware
implementation and can be applied to progressive transmission.
OCIS codes: 100.0100, 100.2000, 100.6890.
Hyperspectral images that have been widely used in mil-
itary and civilian applications are massively large sized
three-dimensional (3D) data sets. Efficient compression
needs to be applied to these data sets in order to re-
duce the storage and bandwidth costs. In recent years,
3D wavelet image compression algorithms based on 3D
set partitioning in hierarchical trees (SPIHT)
[1−3]
and
3D set partitioned embedded block (SPECK)
[4−6]
have
been proposed for progressive hyperspectral image com-
pression. The ordered lists are used in these algorithms
to store the coordinates of significance coefficients and
subsets in the sorting order. The use of lists poses some
drawbacks for hardware implementation in that a large
amount of unfixed memory is needed to maintain these
lists and the operations of the list nodes increase the com-
plexity of algorithms.
In this paper, we extend our recently proposed two-
dimensional (2D) embedded wavelet coder bas ed on sig-
nificance tree splitting
[7]
to three dimensions for h yper-
spectral image compression. We call this new coding
technique 3D significance tree splitting. First, 3D dis-
crete wavelet transform (DWT) is used to exploit the spa-
tial and spectral correlations. Next, the 3D significance
tree structure is constructed from the 3D orientation
tree and the wavelet coefficients are encoded via 3D sig-
nificance tree splitting. This algorithm does not require
lists and it is suitable for hardware implementation.
As hypersp ectral images have a tight statistical de-
pendency along both spatial and spectral directions, 3 D
DWT can exploit spatial and sp ectral correlations. Here,
we first apply 2D dyadic wavelet decomposition on each
spectrum of image, and then apply one-dimensional (1D)
dyadic wavelet decomposition on the spectral dimension.
In the resulting 3D wavelet domain, most of the en-
ergy is concentrated in the low frequency subbands. The
spatial relationship o n the hierarchical pyramid of the
coefficients can b e represented as the 3 D o rientation tree
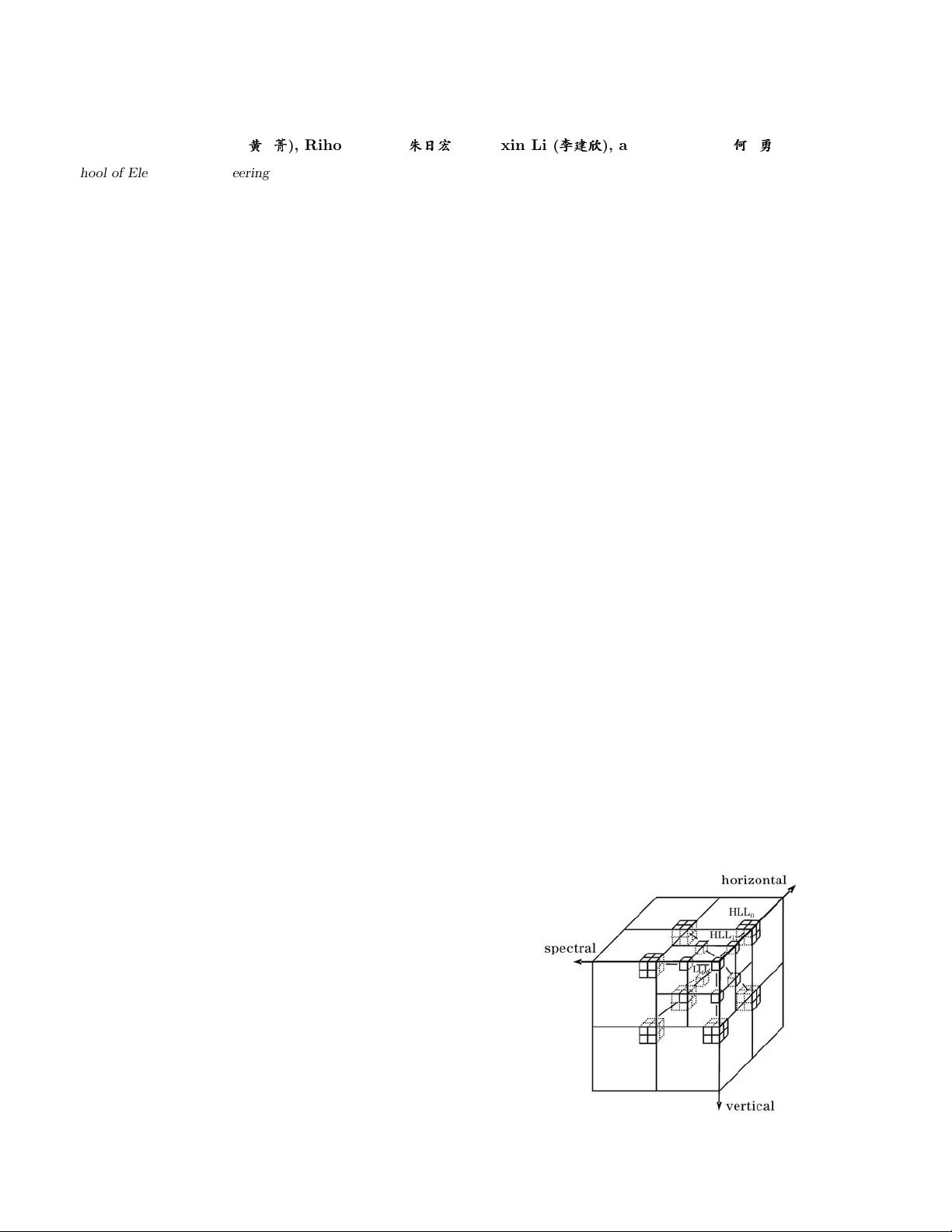
structure. Figure 1 shows the 3D orientation tree struc-
ture after two -level decomposition. All the coefficients
are organized by 3D orientation trees with ro ots located
at the low-low-low (LLL) subband. Each root node in
LLL subband has seven offspring which corr e spond to
the pixels of the seven different spatial orientations at
the next finer scale of the pyramid. Except of the high-
est frequency subbands and LLL subband, each node has
eight o ffspring corresponding to pixels of the same spa-
tial orientation at the next finer level of the pyramid,
and these eight offspring form a group of 2 × 2 × 2ad-
jacent pixels. Let us define O(i, j, k) as the offspring of
the pixel (i, j, k). So for the LLL subband we have
O(i, j, k)={(i, j + h
LLL
,k), (i + w
LLL
,j,k),
(i, j, k + l
LLL
), (i + w
LLL
,j+ h
LLL
,k),
(i + w
LLL
,j,k+ l
LLL
), (i, j + h
LLL
,k+ l
LLL
),
(i + w
LLL
,j+ h
LLL
,k+ l
LLL
)}, (1)
and for the subbands with the exception of the highest
frequency subbands and LLL subband we have
Fig. 1. 3D orientation tree structure.
1671-7694/2007/070393-04
c
2007 Chinese Optics Letters









